Jgtony Developer blog

15 Jul 2019

알고리즘 - 수학

c++

백준 알고리즘 문제들 중 수학에 관한 내용을 정리하였다. 연산, 나머지 구하기, 최대공약수/최소공배수, 소수찾기 등을 다룬다.

나머지를 구하는 문제

계산을 하는 과정 중간중간에 나머지를 구한다

덧셈과 곱셈의 경우 (A+B)%C => (A%C + B%C) % C 이와 같이 각각 계산해서 나머지를 구해도 된다

image.png

뺄셈의 경우 한번 나누는 수로 더해주어야 한다 (a%c - b%c + c)%c

<안중요(참고)> 나눗셈의 경우 (c가 소수이고, a와 b가 서로소인 경우) (a/b)%c => (axb^c-2)%c

최대공약수

ex) 정답이 분수가 나오는데 기약분수로 구하여라

가장 쉬운 방법은 모든 수로 나누어보고 큰것을 고르는 방법인데 좋지 않다 시간복잡도는 a,b중 작은 것을 기준으로 한다면 O(n)

int g = 1;
for (int i=2;i<min(a,b);i++) {
    if(a%i == 0 && b%i == 0) {
        g = i
    }
}

유클리드 호제법 (암기하기)

a 와 b 가 있을 때, 두수의 최대 공약수 GCD(a,b) 는 GCD(b,a%b) 와 같다

ex) GCD(35,21) -> (21,14) -> (14,7) -> (7,0) 이때 7이 최대공약수가 된다

시간복잡도는 O(logN) ex) 재귀함수 사용하기

int gcd(int a, int b) {
    if (b == 0) {
        return a;
    } else {
        return gcd(b,a%b)
    }
}

ex) 재귀를 사용하지 않고

int gcd(int a, int b) {
    while (b!=0) {
        int r = a%b;
        a = b;
        b = r;
    }
    return a;
}

세개의 수도 마찬가지로 반복해서 하면 된다

GCD(a,b,c) => GCD(GCD(a,b),c)

N개의 수도 마찬가지

최소공배수

최대공약수를 유클리드 호제법으로 구한 후 (g) LCM(a,b) = g * (a/g) * (b/g) 이다

두수의 최대공약수로 나누어 유일한 수를 뽑고, 그 둘을 곱한다. 그 곱한 값에 최대공약수를 곱해주면 된다

int LCM(a,b) {
    int oa = a;
    int ob = b;
    while(b!=0) {
        int r = a%b;
        a = b;
        b = r;
    }
    int g = a;

    return g * (oa/g) * (ob/g)
 }

소수

약수가 1과 자기자신밖에 없다

소수가 되려면, 2 이상이고, n-1 이하인 자연수로 나누어 떨어지면 안된다

어떤수가 소수인지 아닌지 판별하기

is it prime number?

아래의 방법은 O(N)

bool prime(int n) {
    if (n<2) { // 소수는 2이상이여야 한다
        return false;
    }
    for (int i=2;i<n-1;i++) {
        if(n%i==0) {// 나누어 떨어지면 소수가 아니다
            return false;
        }
    }
    // 모두 걸리지 않으면 소수이다(이전에 return 되지 않았다면)
    return true;
}

**<좀더 빠른="" 방법="">**

2이상이고 N/2 이하인 자연수로 나누어 떨어지면 안된다.

시간복잡도는 O(N)

bool prime(int n) {
    if (n<2) { // 소수는 2이상이여야 한다
        return false;
    }
    for (int i=2;i<n/2;i++) {
        if(n%i==0) {// 나누어 떨어지면 소수가 아니다
            return false;
        }
    }
    // 모두 걸리지 않으면 소수이다(이전에 return 되지 않았다면)
    return true;
}

<가장 좋은="" 방법="">(암기하기)

2이상이고 루트N 이하인 자연수로 나누어 떨어지면 안된다.

시간복잡도 O(루트N)

만약 소수가 아니면 N은 두수의 곱으로 이루어질 것이기 때문에 a * b = n 이라면 a<= 루트n 이거나 b>= 루트n 이다. 즉 둘중에 하나는 루트n보다 작고, 하나는 루트n 보다 크다. 따라서 소수가 아니라면 루트n 보다 작은 값에서 나누어 떨어질 것이고, 그렇지 않다면 a * b = 루트 n 으로 이루어지지 않는다는 것을 의미한다.(소수이다)

bool prime(int n) {
    if (n<2) { // 소수는 2이상이여야 한다
        return false;
    }
    for (int i=2;i*i<=n;i++) { // 소수가 나오는 것은 좋지 않기에 i*i 로 표현
        if(n%i==0) {// 나누어 떨어지면 소수가 아니다
            return false;
        }
    }
    // 모두 걸리지 않으면 소수이다(이전에 return 되지 않았다면)
    return true;
}

N보다 작거나 같은 모든 소수 찾기

find all prime number

항상 O(루트) 보다 O(log) 가 좋다. 따라서 위의 소수를 구하는 방법보다, 새로운 방법을 채택한다

에라토스테네스의 체(암기하기)

이전 단계에서 지워지지 않은 것은 즉 자기 자신보다 작은 수로 지워지지 않았기 때문에 소수이다.

먼저 2의 배수를 지운다 (지워지지 않은 수 중 가장 작은 수이기 때문)

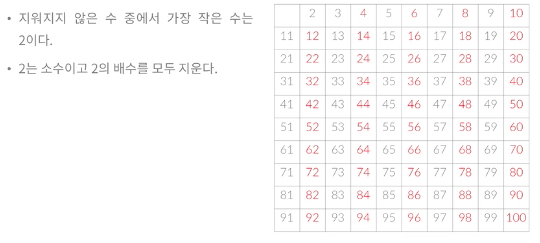
image.png

그 다음으로 지워지지 않은 수 중 가장 작은 수는 3이므로 3의 배수를 지운다

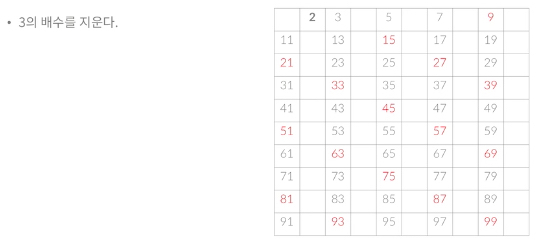
image.png

마찬가지로 지워지지 않은 수 중 가장 작은 수인 5를 지우고, 7을 지우고, 모두 진행한 다음 남아있는 수들이 소수이다.

실제 코드이다 실제로 배열에서 지우고 하는 방법은 느리다! 그저 지워졌는지 아닌지 확인만 하는 방법으로 진행해야 한다.

시간복잡도는 O(N * log(logN))

int prime[100]; // 소수 저장
int pn = 0; // 소수의 개수를 카운트
bool check[101]; // 지워졌다면 true 로 바꾼다. 초기화는 false
int n = 100; // 100까지의 소수
for(int i=2; i<=n; i++) {
    if(check[i] == false) {
        prime[pn++] = i;
        for(int j = i+i; j<=n; j+=i) {
            check[j] = true;
        }
    }
}

m 이상 n 이하의 소수를 출력하기

에라토스테네스의 체로 구한 후 m 이상인 것만 출력

골드바흐의 추측

2보다 큰 모든 짝수는 소수의 합으로 표현가능하다

ex) 백만 이하의 짝수에 대해 골드바흐의 추측을 검증한다

=> 모든 소수를 구하고, 이것과 어떤 합이 짝수가 되는지 확인

에라토스테네스의 체에서 check 배열을 검사하여 소수인지 아닌지 확인할 수 있다.



문제 10430: 나머지 구하기

38015DE5-129A-486C-8C6A-C1C1F6330541.png

코드

#include <stdio.h>
int main() {
    int a,b,c;
    scanf("%d %d %d",&a,&b,&c);
    printf("%d\n%d\n%d\n%d",(a+b)%c,(a%c+b%c)%c,(a*b)%c,(a%c*b%c)%c);
}

문제 2609: 최대공약수와 최소공배수

B93DE90E-6EB5-45CE-982D-7F747F7F8EF4.png

#include <stdio.h>
int main() {
    int a,b,r,oa,ob;
    scanf("%d %d",&a,&b);
    oa = a;ob = b;
    while(b!=0) {
        r=a%b;a=b;b=r;
    }
    printf("%d\n%d",a,a*(oa/a) * (ob/a));
}

문제 1934: 두 수의 최소공배수

8FECD764-B583-4C11-95CE-A7074DD1374E.png

#include <stdio.h>
int g(int a,int b) {return b?g(b,a%b):a;}
int main(){
    int T,A,B;
    scanf("%d",&T);
    while(T--) {
        scanf("%d%d",&A,&B);
        printf("%d\n",A*B/g(A,B));
    }
}

문제 9613: 모든 GCD의 합

E0326E11-24EB-4BD6-B13A-DD8198C9ADCC.png

#include <stdio.h>
#include <vector>
using namespace std;
int g(int a,int b) {
    return b?g(b,a%b):a;
}
int main() {
    int t,n;
    scanf("%d",&t);
    while(t--) {
        scanf("%d",&n);
        vector<int> a(n);
        for(int i=0;i<n;i++) {
            scanf("%d",&a[i]);
        }
        long long sum=0;
        for(int i=0;i<n;i++) {
            for(int j=i+1;j<n;j++) {
                sum += g(a[i],a[j]);
            }
        }
        printf("%lld\n",sum);
    }
}

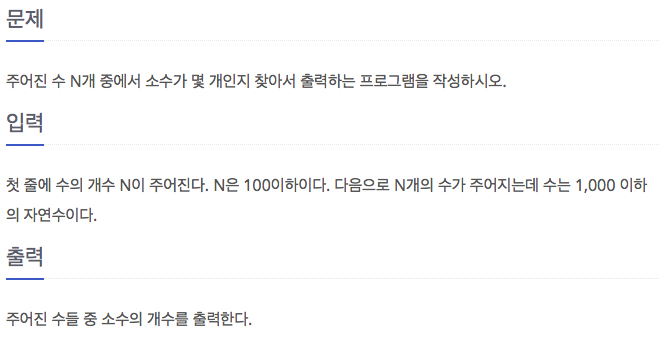
문제 1978: N 이하의 소수의 개수

F6D2D4E1-0402-4552-BBDE-086D93AC9094.png

#include <stdio.h>
#include <vector>
bool p(int a){
    if (a<2) return false;
    else if(a==2) return true;
    for(int i=2;i*i<=a;i++) {
        if(a%i==0) return false;
    }
    return true;
}
int main() {
    int n,ct=0;
    scanf("%d",&n);
    std::vector<int> a(n);
    for(int i=0;i<n;i++) scanf("%d",&a[i]);
    for(int i=0;i<n;i++) {
        if(p(a[i])) ct++;
    }
    printf("%d",ct);
}

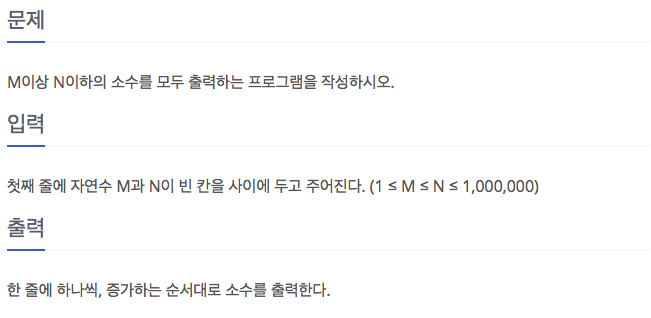
문제 1929: M이상 N이하의 모든 소수

29F7ACD8-1404-468C-AE2E-EA2209488040.png

#include <stdio.h>
#include <vector>
int main() {
    int m,n;
    scanf("%d %d",&m,&n);
    std::vector<bool> c(n);
    int p[n],ct=0;
    for(int i=2;i<=n;i++) {
        if(!c[i]) {
            if(i>=m) p[ct++] = i;
            c[i] = true;
            for(int j=i+i;j<=n;j+=i) c[j] = true;
        }
    }
    for(int i=0;i<ct;i++) printf("%d\n",p[i]);
}

문제 6588: 골드바흐의 추측

4FFC44F1-C0EA-4387-A652-E3C721AC78D7.png

7AC75292-426D-4561-8503-93104A5BBDDA.png

#include <stdio.h>
#include <vector>
int main() {
    int max = 1000000;
    std::vector<bool> c(max);
    int n;
    int p[max];
    int ct=0;
    for(int i=2;i<=max;i++) {
        if(!c[i]) {
            p[ct++] = i;
            for(int j=i+i;j<=max;j+=i) {
                c[j] = true;
            }
        }
    }
    while(true) {
        bool f = false;
        scanf("%d",&n);
        if(n==0) break;
        for(int i=0;i<ct;i++) {
            if(!c[n-p[i]]) {
                printf("%d = %d + %d\n",n,p[i],n-p[i]);
                f = true;
                break;
            }
        }
        if(!f) printf("Goldbach's conjecture is wrong.");
    }
}

Other Posts

Comments