알고리즘 - 브루트 포스
백준 알고리즘 문제들 중 브루트 포스에 관한 내용을 정리하였다. 브루트 포스 문제는 모든 경우의 수를 구하는 방법인데, 이때 문제를 성공적으로 풀어내기 위해서는 시간복잡도를 미리 계산해보고 가능한 접근인지 확인해야 한다.
브루트 포스
있는 그대로 모든 경우의 수를 구하는 것을 말한다. 문제 그대로 답을 찾는 모든 방법을 동원하기 때문에, 그 방법의 경우의 수가 너무 크다면 시간제한에 의해 풀 수 없는 문제가 되어버린다
따라서 브루트 포스에서는 경우의 수의 숫자가 굉장히 중요하다
먼저 문제의 경우의 수를 계산해 보고 몇백만 정도의 가짓수가 나온다면 시도해도 좋다
일곱난쟁이(2309번 문제)
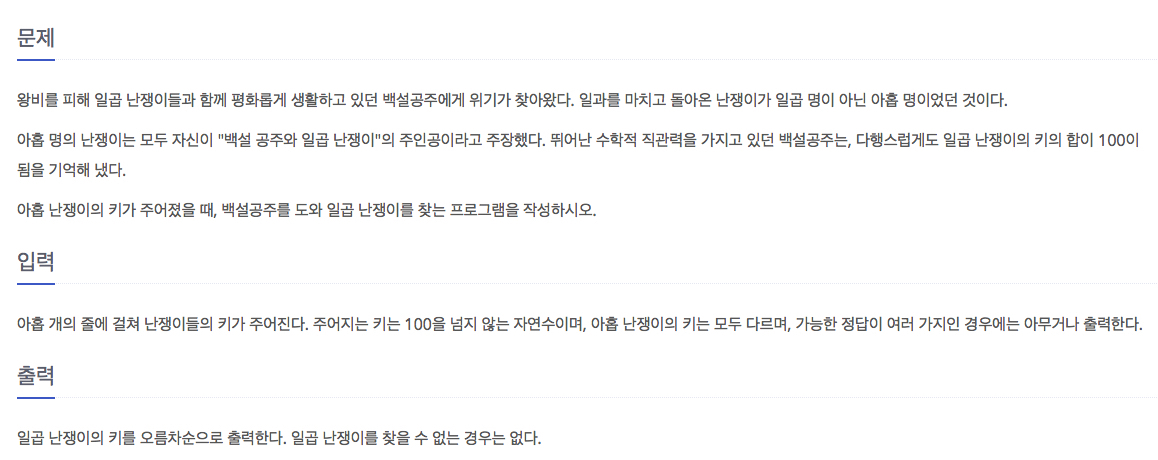
이 문제는 9명의 난쟁이 중 7명의 난쟁이 키의 합이 100이 되어야 한다.
9명 중 7명을 뽑는 것인데, 반대로 말하면 9명 중 2명을 뽑아서 나머지의 합이 100이면 된다.
따라서 모든 경우의 수는 9C2 이므로 9*8/2 = 36 가지가 된다. 충분히 일일이 구할 수 있다
나머지의 합이 100이 되어야 하므로 먼저 모든 난쟁이의 키의 합을 sum 으로 구해놓고, 이중 for문을 사용해 전체에서 2명의 난쟁이를 제외한 키의 값이 100이 되면 된다
코드는 다음과 같다.
#include <stdio.h>
#include <algorithm>
int main() {
int n = 9,a[n],sum=0;
for(int i=0;i<n;i++) {
scanf("%d",&a[i]);
sum += a[i];
}
std::sort(a,a+9);
for(int i=0;i<n;i++) {
for(int j=i;j<n;j++) {
if(sum-a[i]-a[j]==100) {
for(int k=0;k<n;k++) {
if(k!=i && k!=j) {
printf("%d\n",a[k]);
}
}
return 0;
}
}
}
}오름차순으로 출력하라고 했기 때문에 #include <algorithm> 의 sort() 를 사용하였다.
실제로 for 문은 3개가 들어갔지만 마지막 포문은 한번만 실행되고 return 되기 때문에(찾으면 끝내면 됨) 시간복잡도는 O(N^2) 가 된다.
날짜계산(1476번 문제)

E, S, M 의 규칙을 파악하고 푸는 문제이다. y년수가 올라갈수록 E 와 S 와 M 은 각각 %15, %28, %19 의 값과 같다. 단 나머지가 0 인 경우는 각각 15,28,19 로 나타난다.
코드는 다음과 같다
#include <stdio.h>
int main() {
int e,s,m,re,rs,rm;
scanf("%d %d %d",&e,&s,&m);
for(int y=1;;y++) {
if(y%15==0) re=15; else re=y%15;
if(y%28==0) rs=28; else rs=y%28;
if(y%19==0) rm=19; else rm=y%19;
if(re==e && rs==s && rm==m) {
printf("%d",y);
break;
}
}
}사실 이렇게 말고 16으로 나머지를 구하고 더 이쁜 규칙을 찾아보려다가..시간 엄청날리고 회의감이 들어서 그냥 이렇게 했다. 결과적으로 수가 적어서 빠르긴 하다.
테트로미노 (14500번 문제)

접근법
먼저 m * n 의 판에 각 블록이 들어갈때 어떤 경우의 수를 가지게 되는지 계산한다.
각 블록 당 모양은 회전을 포함하여 19개가 존재하고, 각 블록이 판에 들어갈 수 있는 가지수는 mn 이하이기 때문에 총 경우의 수는 19 * mn 이다. mn 은 최대 25000 까지 나올 수 있기 때문에 경우의 수는 약 500만 이하가 된다.
이 문제는 접근법만 간단하게 하면 쉽게 풀리는 문제다. 먼저 n * m 판을 만들고, 그 위에 모든 종류의 도형을 올려놓고 최대값을 찾으면 되는 문제이다. 도형을 만들 때는, 기준 시작점을 정하고, 그 기준으로 도형의 모양을 배열로 구축한다. 전체 판을 한칸씩 돌며, 기준점에 해당하는 도형을 놓고(놓을 수 없는지도 확인 = 예외처리) 각 값들을 모두 더하고 최대값을 구하면 된다.
코드는 다음과 같다
#include <stdio.h>
#include <vector>
using namespace std;
int main() {
int n,m;
scanf("%d %d",&n,&m);
vector<vector<int> > p(n, vector<int>(m));
for(int i=0;i<n;i++) {
for(int j=0;j<m;j++) scanf("%d",&p[i][j]);
}
int a[19][3][2] = {
{{0,1}, {0,2}, {0,3}},
{{1,0}, {2,0}, {3,0}},
{{1,0}, {1,1}, {1,2}},
{{0,1}, {1,0}, {2,0}},
{{0,1}, {0,2}, {1,2}},
{{1,0}, {2,0}, {2,-1}},
{{0,1}, {0,2}, {-1,2}},
{{1,0}, {2,0}, {2,1}},
{{0,1}, {0,2}, {1,0}},
{{0,1}, {1,1}, {2,1}},
{{0,1}, {1,0}, {1,1}},
{{0,1}, {-1,1}, {-1,2}},
{{1,0}, {1,1}, {2,1}},
{{0,1}, {1,1}, {1,2}},
{{1,0}, {1,-1}, {2,-1}},
{{0,1}, {0,2}, {-1,1}},
{{0,1}, {0,2}, {1,1}},
{{1,0}, {2,0}, {1,1}},
{{1,0}, {2,0}, {1,-1}},
};
int r = 0;
for(int i=0;i<n;i++) {
for(int j=0;j<m;j++) {
for(int k=0;k<19;k++) {
if(i+a[k][0][0] < 0 || i+a[k][0][0] > n-1 || i+a[k][1][0] < 0 || i+a[k][1][0] > n-1 || i+a[k][2][0] < 0 || i+a[k][2][0] > n-1) continue;
if(j+a[k][0][1] < 0 || j+a[k][0][1] > m-1 || j+a[k][1][1] < 0 || j+a[k][1][1] > m-1 || j+a[k][2][1] < 0 || j+a[k][2][1] > m-1) continue;
int sum = p[i][j] + p[i+a[k][0][0]][j+a[k][0][1]] + p[i+a[k][1][0]][j+a[k][1][1]] + p[i+a[k][2][0]][j+a[k][2][1]];
if(sum > r) r = sum;
}
}
}
printf("%d",r);
}
123 더하기(9095번 문제)
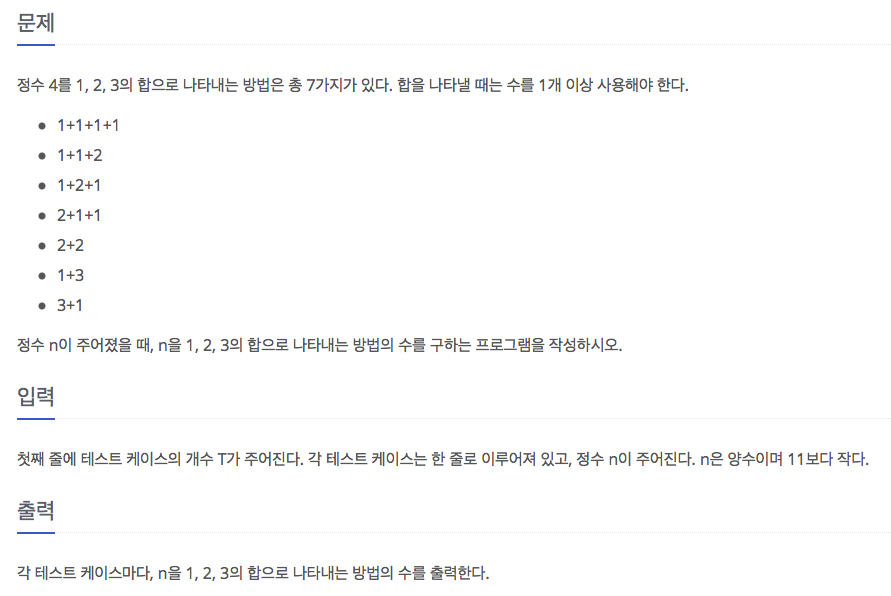
이 문제는 숫자 n 이 주어지고 1,2,3 으로 만들 수 있는 경우의 수를 출력하는 것이다. 완전 그냥 다 구하면 되는데, n 이 1개의 숫자로 이루어질 경우, 2개로 이루어질경우 …. n개로 이루어질 경우를 모두 나누어서 n 중 for 문으로 감싸주면 된다.
코드는 너무 더러워서 생략한다.
순열
1~N까지로 이루어진 수열 겹치는 숫자가 존재하지 않고 순서가 중요한 문제 에서 사용된다
크기가 N인 순열은 N!개가 존재한다. (옵션 : 사전순으로 나열한다) 사전순으로 나열하였을 때 첫순열은 오름차순으로 구성되고 마지막 순열은 내림차순이다.
N = 3 인경우 첫순열은 1 2 3 마지막 순열은 3 2 1 그렇다면 중간의 순열은 어떻게 구할까?
다음순열을 알아보는 방법 C++ STL algorithm 에는 이미 next_permutation 과 prev_permutation 이 있다.
예를들어 N=7 인 순열중 m번째에 2 3 1 7 6 5 4 가 있다고 하자 이 수는 2 3 1 로 시작하는 순열중 마지막 순열이라고 할 수 있다 (7 6 5 4 가 내림차순이기 때문에) 그렇다면 m+1번째 순열은 2 3 4 1 5 6 7 이 된다.
일반화하기
첫번째로 어떤 순열이 있을 때 어떤 그룹의 마지막 순열인지를 찾아내야 한다.
앞에서 본 것처럼 마지막 순열은 내림차순으로 존재한다
7 2 3 6 5 4 1 7 2 3 6 5 4 1 i = 4
끝의 자리부터 순서대로 A[i-1] > A[i] 인 가장 큰 i 를 찾는다 (즉 A[i-1] <= A[i] 인 수까지 찾기) 이렇게 찾아진 i 는 내림차순이 시작하는 자리수라고 할 수 있다.
7 2 3 6 5 4 1 7 2 3 6 5 4 1 7 2 4 1 3 5 6
이렇게 내림차순이 시작하는 그룹 = 그 그룹의 마지막 순열을 찾았다면, 이제 바로 그다음 순열을 찾는다. 바로 그 다음 순열은 i-1 번째 자리를 뒤에 있는 수들 중 더 크면서 가장 작은 수로 바꾸어야 한다.
다음순열을 찾는 과정은 다음과 같이 단순화하여 표현할 수 있다.
- 어떤 그룹의 끝순열을 찾고 (i 를 찾음) -> O(N)
- 그 다음 순열을 찾기 위해 i-1번째 문자와 i~ 문자를 바꾸고 -> O(N)
- i 이후의 문자들을 오름차순으로 정렬한다 -> O(N)
크기가 n인 배열이 a에 담겨있다고 생각한다
bool next_permutation(int * a, int n) {
int i = n-1;
while (i>0 && a[i-1] >= a[i]) i -= 1;
if(i<=0) return false;
int j = n-1;
while(a[j] <= a[i-1]) j-=1;
swap(a[i-1],a[j]);
j = n-1;
while(i<j) {
swap(a[i],a[j]);
i += 1;
j -= 1;
}
return true;
}다음 순열 (10972번 문제)
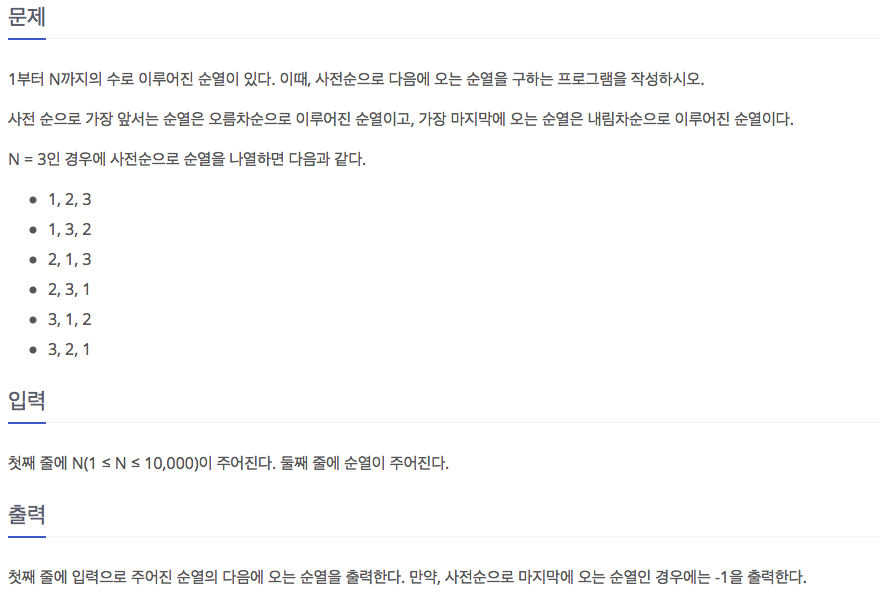
이 문제는 STL algorithm 의 next_permutation 을 사용하면 쉽게 풀 수 있다. 특징적으로 알아야 할 부분은, next_permutation 이 다시 첫 순열로 돌아가게 되면 bool flag 를 0(false) 로 return 한다는 것이다. 이것을 이용해서 쉽게 코드를 짤 수있다.
코드는 다음과 같다
#include <stdio.h>
#include <vector>
#include <algorithm>
int main() {
int n;
scanf("%d",&n);
std::vector<int> a(n);
for(int i=0;i<n;i++) scanf("%d",&a[i]);
if(std::next_permutation(a.begin(),a.end())==0) {
printf("%d",-1);
return 0;
}
for(int i=0;i<n;i++) printf("%d ",a[i]);
}
이전 순열의 경우
다음 순열의 반대로 해주면 된다. 즉 마지막 순열을 찾고 그다음 순열을 찾았던 것의 반대로, 첫 순열을 찾고 그 전 순열을 찾는 방식을 취한다.
7 1 5 2 3 4
첫순열을 찾는 방법은, a[i-1] <= a[i] 인 가장 큰 i 를 찾아주면 된다.
위의 예시에서는 i = 3
그 후 a[i-1] 과 비교해서 a[i-1] 보다 작은 녀석들 중 가장 큰 수와 바꾼다.
7 1 5 2 3 4 a[2] 와 a[5] 를 바꾼다. 7 1 4 2 3 5
마지막으로 a[i] 번째 이상의 수들을 내림차순으로 바꾼다.
7 1 4 5 3 2
이전순열(10973번 문제)
10972 번 문제와 완전히 동일하나, 이전 순열을 출력하는 문제이다. 이건 next_permutation 을 prev_permutation 으로 바꾸어 주기만 하면 된다.
코드는 다음과 같다
#include <stdio.h>
#include <vector>
#include <algorithm>
int main() {
int n;
scanf("%d",&n);
std::vector<int> a(n);
for(int i=0;i<n;i++) scanf("%d",&a[i]);
if(std::prev_permutation(a.begin(),a.end())==0) {
printf("%d",-1);
return 0;
}
for(int i=0;i<n;i++) printf("%d ",a[i]);
}모든순열을 구하는 방법(암기하기)
- 첫순열을 만든다 (all 오름차순)
- 다음순열이 존재하지 않을 때까지 다음순열을 구한다
알고리즘 문제에서 다음 순열을 구하는 next_permuation 을 사용할때는 주로 do-while 문을 사용한다 next_permutation 이 다음순열을 만들어 주고 있는지 없는지도 확인해 주기 때문에 위에 조건을 작성하면 첫 순열이 나타나지 않기 때문이다.
모든 순열(10974번 문제)
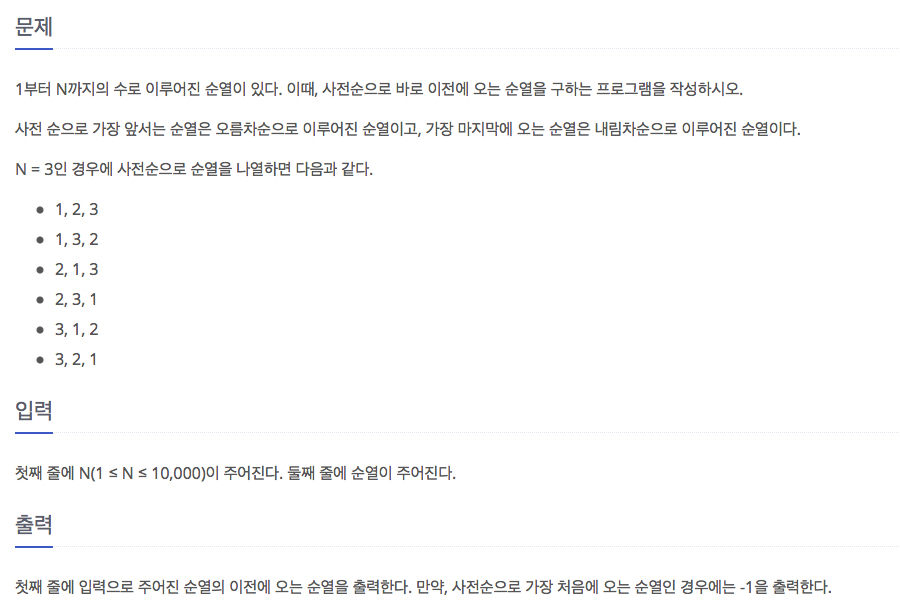
여기서 주의할 점은 do-while 문으로 다음 순열이 첫순열로 돌아오기 전까지 진행해야 한다는 것이다.
코드는 다음과 같다
#include <stdio.h>
#include <vector>
#include <algorithm>
int main() {
int n;
scanf("%d",&n);
std::vector<int> a(n);
for(int i=0;i<n;i++) a[i] = i+1;
do {
for(int i=0;i<n;i++) printf("%d ",a[i]);
printf("\n");
} while(std::next_permutation(a.begin(),a.end()));
}
차이를 최대로(10819번 문제)
문제 : 배열의 크기가 N인 배열은 A에 들어가 있다. 배열의 순서만 바꾸는 것이 가능하다.

어떻게 구할 수 있을까?
접근법
N 의 수가 8보다 작으므로 모든 경우의 수를 싹 다 구한다. (yeah brute..)
그냥 문제 내용 그대로 코드를 작성하고 가장 큰 녀석을 구한다.
sort(a);
do {
int temp = calculate(a);
result = max(result, temp);
}while(next_permutation(a.begin(),a.end());외판원 순회2(TSP 문제)
Travelling Salesman Problem

여기서 눈여겨 보아야 할 부분은 "다시 방문이 불가" == 순열 , N개의 모든 도시를 거쳐야 한다 이다. 이는 즉 순열을 사용해서 풀 수 있다는 것을 알려준다. 또한 N의 제한이 10 이하여야 1초~2초 이내에 순열을 사용하여 풀어낼 수 있다.
다행히도 이 문제에서는 N의 제한이 10 이하이기 때문에 모든 경우의 수를 구한 뒤, 가장 적은 cost 가 드는 경로를 찾아 낼 수 있다.
d 에는 도시의 순서 배열이 들어있다고 가정하자
do {
bool ok=true;
int sum = 0;
for (int i=0; i<n-1; i++) {
if(w[d[i]][d[i+1]] == 0) ok = false;
else sum += w[d[i]][d[i+1]];
}
if (ok && w[d[n-1]][d[0]] != 0) {
sum += w[d[n-1]][d[0]];
if (result > sum) result = sum;
}
}while(next_permutation(d.begin(), d.end()));외판원 순회 문제의 경우 조금더 생각해 볼 것이 있다.
1 2 3 4 2 3 4 1 3 4 1 2 4 1 2 3
위의 4가지 순서들은 다 같은 경우라고 할 수 있다. 즉 시작점을 임의로 지정(고정) 하고 시작해도 된다
맨 앞을 고정하고 순열을 만드는 경우는 위의 코드에서 while(next_permutation(d.begin()+1, d.end())); 로 바꾸어 주면 된다. 그러면 맨 앞의 순서는 고려하지 않고 나머지 순서들만을 순열로 계산하게 된다.
다른 방법으로는 시작점을 임의로 고정하고 그 시작점이 처음에 나왔을 때는 검사하지 않는 코드를 첨가해 줄 수도 있다. if (d[0] != 1) break; 이 코드를 추가해 주면 시작점이 1인 순열은 검사하지 않는다.
로또
같은 수가 있는 경우??? 그래도 next_permutation 이 정상적으로 동작한다.

전체 경우의 수는 5! / (2! * 3!) 의 경우의 수가 나오게 된다.
문제 : 입력으로 주어진 K개의 수 중에서 6개의 수를 고르기
위와 같은 문제를 순열로 풀려면, 고르는 수의 개수가 정확하게 정해져 있어야 한다
모든 수들 중 골라진 수는 1, 골라지지 않는 수는 0 으로 생각하면 => K개의 수 중 1이 6개, 0이 K-6 개라고 생각하고 푼다.
연산자 끼워넣기


N개의 수와 N-1 개의 연산자가 있다.
접근법
연산자의 순서만 바뀌는 것을 알 수 있다. 연산자의 개수도 정해져 있다. 따라서 연산자의 순서를 수열로 계산하면 된다. permutation 을 돌면서 가장 큰 값을 모두 다 구해보는 방식으로 풀 수 있다.
연산자의 개수도 10개 이하이고, 순서가 정해져 있기 때문에 충분히 구할 수 있다.
Comments