알고리즘 - 그래프
알고리즘 문제에서 가장 기본이 되고 가장 중요한 그래프와 BFS 에 관한 개념 문제이다. 로직을 알고 있더라도 까먹는 경우가 발생하므로 반드시 코드의 구조를 익숙한 방식으로 암기하는 것이 중요하다.
그래프 문제를 푸는 접근법
- 인접행렬을 구한다 : 모든 관계를 모든 행렬로 표현한다
- 인접리스트를 구한다 : 한 정점에서 갈수있는 노드들을 행렬로 저장한다.
대부분 인접리스트를 구하는 것이 cost 가 적게 들기 때문에, 문제에서 직접 행렬을 제시해준 경우 빼고는 인접리스트로 풀도록 하자.
BFS와 DFS (1260번 문제)
전형적으로 BFS와 DFS를 구하는 문제이다.
먼저 상대적으로 쉬운 DFS는 다음과 같은 특징을 암기하자.
DFS
- 기본적으로 재귀함수를 사용해서 푼다
- 하나의 노드로부터 갈수있는 모든 노드로 dfs 를 돌린다
여기에서 “갈수있는” 이라는 뜻은, 이미 지나왔던 노드인지 확인하는 것이다
즉 코드는 다음과 같은 형태를 띄게 된다
void dfs(int start) {
// 이제 이 노드를 돌기 때문에 check 해준다
check[start] = true;
// a는 인접리스트가 저장되어 있다(a[start]의 사이즈만큼 돌린다)
for(int i=0;i<a[start].size();i++) {
// 아직 방문하지 않은 점이라면, 방문한다
int next = a[start][i];
if(check[next] == false) {
dfs(next);
}
}
}BFS
- queue 를 사용해서 앞에 있는 queue.front() 부터 시작한다.
- while(!q.empty()) 를 사용해서 queue 가 비어질때까지 반복한다.
여기서 중요한 점은 시작점을 queue 에 넣어야 한다는 것이다
#include <queue>
void bfs(int start) {
queue<int> q;
check[start] = true;
q.push(start);
while(!q.empty()) {
int front = q.front()
q.pop();
for(int i=0;i<a[front].size();i++) {
int next = a[front][i];
if(check[next] == false) {
check[next] = true;
q.push(next);
}
}
}
}
연결요소의 개수(11724번 문제)
그래프에서 이어져 있는 그룹을 연결 요소라고 한다. 어떤 그래프를 보고 연결 요소의 개수를 구하는 문제이다.
이 문제 같은 경우, BFS 또는 DFS 를 몇번 돌려야만, 모든 노드들이 모두 check 되는지를 확인하면 된다.
코드는 다음과 같다
// 메인 함수에서 처음부터 dfs 를 loop 로 돌린다
int ct = 0;
for(int i=1;i<=n;i++) {
if(check[i]==false) {
dfs(i);
ct++;
}
}
printf("%d",ct);
이분그래프(1707)
이분그래프는 하나의 정점에서 다른 정점으로 이동할때, 확실히 다른 그룹 이어야 한다는 것이다. 즉 색으로 표시하자면 빨강 정점은 항상 파랑 정점과 이어져 있고, 파랑 정점은 항상 빨강 정점과 이어져 있다는 것이다.
이 문제에서 그래프가 이분 그래프인지를 알아보려면, 재귀 dfs 를 사용할때 현재 정점에 색을 칠하고, 다음으로 가는 정점에 파란색을 칠하는 과정을 수행해야 한다.
기존에 check 배열이 true 와 false 만을 가졌다면, 이제는 0(지나지 않음), 1(빨강), 2(파랑) 으로 체크해주면 된다. 그리고 마지막에 더이상 갈 정점이 없을 때, 이어져 있는 정점이 현재 색과 다른 점인지를 확인해 주면 된다. 만약 모두 번갈아서 나온다면 이분 그래프가 맞다.
주의! 여러 테스트 케이스가 진행될 때마다 전역 변수 check 와 인접리스트 a 는 초기화를 시켜 주어야 한다. 또한 이 그래프는 연결요소가 몇개 있는지 모르기 때문에 모든 경우의 dfs 또는 bfs 를 구해 보아야 한다.
#include <stdio.h>
#include <algorithm>
#include <vector>
using namespace std;
vector<int> a[20001];
int check[20001];
bool flag = true;
void dfs(int start,int color) {
check[start] = color;
for(int i=0;i<a[start].size();i++) {
int next = a[start][i];
if(check[next]== 0) {
dfs(next,3-color);
}
}
}
int main() {
int k;
scanf("%d",&k);
while(k--) {
flag = true;
int v,e,v1,v2;
scanf("%d %d",&v,&e);
for (int i=1; i<=v; i++) {
a[i].clear();
check[i] = 0;
}
for(int i=0;i<e;i++) {
scanf("%d %d",&v1,&v2);
a[v1].push_back(v2);
a[v2].push_back(v1);
}
for(int i=1;i<=v;i++) {
if(check[i]==0) {
dfs(i,1);
}
}
for(int i=0;i<v;i++) {
for(int j=0;j<a[i].size();j++) {
if(check[i]==check[a[i][j]]) {
flag = false;
}
}
}
printf("%s\n",flag? "YES":"NO");
}
}특히나 이 문제에서 주의해야 할 점은, 마지막에 모든 인접 리스트를 검사해서 a[i] 에 있는 모든 원소들의 색이 i 와 달라야 한다는 것이다.check[i]==check[a[i][j]] 인지 확인해야 한다.
단지번호붙이기 (2667번 문제)
연결요소의 개수를 구하는 문제와 완벽하게 동일하다. 특이한 점은 미리 인접행렬이 나와있다는 점(이걸 사용하면 됨), 또 노드 끼리 이어져 있는 방향이 4방향(위,아래,왼쪽,오른쪽) 이라는 점이다.
하나의 노드에서 연결되어 있는 노드를 확인 할 때, 4방향을 for 문으로 탐색하면 된다. 만약 아직 check 되지 않은 곳(이 문제에서는 값이 1)이라면 탐색하고, 갈 수 없는 곳(이 문제에서는 값이 0) 이라면 넘어가면 된다.
주의할 점은 4방향의 연결된 노드를 탐색하기 전에, 그 값이 행렬의 범위를 벗어나는지 확인해 보아야 한다. 또한 단지의 크기를 구하기 위해서 dfs 가 한번 돌 때마다 카운트를 증가시켜야 하고, main 에서 dfs 를 실행할 때마다 단지의 개수(연결요소의 개수)를 증가시키는 작업을 동시에 해야 한다.
#include <stdio.h>
#include <vector>
#include <algorithm>
using namespace std;
int p[26][26];
bool check[26][26];
int dx[] = {0,0,1,-1}; // 탐색 방향을 저장해 둔다.
int dy[] = {1,-1,0,0}; // 4방향을 나타낸다.
vector<int> danzi;
int dct = 0;
int n;
void dfs(int x,int y) {
dct++; // 노드를 거칠 때마다 단지의 크기를 증가시킨다.
check[x][y] = true;
for(int i=0;i<4;i++) {
// 유효한 행렬 범위인지 확인하고 dfs 를 진행한다.
if(x+dx[i]>=0 && x+dx[i]<n && y+dy[i]>=0 && y+dy[i]<n) {
if(p[x+dx[i]][y+dy[i]]==1 && check[x+dx[i]][y+dy[i]]==false) {
dfs(x+dx[i],y+dy[i]);
}
}
}
}
int main() {
scanf("%d",&n);
for(int i=0;i<n;i++) {
for(int j=0;j<n;j++) {
scanf("%1d",&p[i][j]);
}
}
int ct = 0;
for(int i=0;i<n;i++) {
for(int j=0;j<n;j++) {
if(p[i][j]==1 && check[i][j]==false) {
dfs(i,j);
danzi.push_back(dct);
// 단지의 크기를 초기화 시켜주고, 단지의 개수를 증가시킨다.
dct = 0;
ct++;
}
}
}
printf("%d\n",ct);
sort(danzi.begin(),danzi.end());
for(int i=0;i<danzi.size();i++) {
printf("%d\n",danzi[i]);
}
}
섬의 개수 (4963번 문제)
이 문제는 단지 구하기 문제랑 완전 똑같은 문제인데, 조금 더 업그레이드 된 버전이다. 이전 문제가 4방향의 연결된 노드를 탐색하며 진행한다면, 이번에는 대각선까지 포함하여 8방향으로 진행된다.
여기서도 마찬가지로 주의할 점은 8가지 방향을 탐색할 때, 배열의 범위를 잘 파악해주는 것이다.
코드는 다음과 같다.
#include <stdio.h>
#include <algorithm>
#include <vector>
using namespace std;
int w,h;
int p[50][50];
bool check[50][50];
int dx[] = {-1,0,1,1,1,0,-1,-1};
int dy[] = {-1,-1,-1,0,1,1,1,0};
void dfs(int x, int y) {
check[x][y] = true;
for(int i=0;i<8;i++) {
int nx = x+dx[i];
int ny = y+dy[i];
if(nx>=0 && nx<h && ny>=0 && ny<w) {
if(check[nx][ny]==false && p[nx][ny]==1) {
dfs(nx,ny);
}
}
}
}
int main() {
while(true) {
for(int i=0;i<50;i++) {
for(int j=0;j<50;j++) {
p[i][j] = 0;
check[i][j] = false;
}
}
scanf("%d %d",&w,&h);
if(w==0 && h==0) break;
for(int i=0;i<h;i++) {
for(int j=0;j<w;j++) {
scanf("%1d",&p[i][j]);
}
}
int ct = 0;
for(int i=0;i<h;i++) {
for(int j=0;j<w;j++) {
if(check[i][j]==false && p[i][j]==1) {
dfs(i,j);
ct++;
}
}
}
printf("%d\n",ct);
}
}본격적인 BFS
BFS는 모든 가중치가 1일때, 최단거리를 구하는 알고리즘이다
- 최단거리 문제 (최소 비용 문제) : 간선의 가중치가 1이어야 한다
- 정점과 간선의 개수가 적어야 한다(시간제한, 메모리제한)
다음은 BFS 의 문제이다.
미로 탐색 (2178번 문제)
가장 빠른 길을 구하는 문제이다.
DFS 는 시작에서 도착으로 갈수 있냐 없냐 만 판단하기 때문에 이 문제를 해결할 수 없다. DFS 는 매번 가능한 모든 경우 중 하나를 선택해서 끝까지 갔다가, 다시 돌아오는 방식을 취하기 때문에, 가장 빠른 길을 구할 수 없다.
BFS 는 시작에서 도착까지 방문한 칸의 최소개수인 경로를 구할 수 있다. 왜냐하면 BFS 는 한꺼번에 한 정점에서 가능한 노드를 그다음 큐에 넣고, 동시에 진행하기 때문에, 몇번째 시도에서 도착 노드에 도달했는지 파악 할 수 있으며, 이게 즉 최소 거리(개수) 가 된다.
이 문제에서 중요한 점은, 하나의 정점에서 다른 갈 수 있는 정점들을 찾을 때, 이존의 cost(값) 에서 1씩 더해주며 다음 정점들에 값을 할당해야 한다는 것이다. 즉 BFS의 탐색에서 다음 노드를 찾으면 기준 노드의 값 + 1 을 할당해 준다는 것이다.
설명이 어려우니 아래의 코드를 보고 이해하자
#include <stdio.h>
#include <queue>
#include <vector>
#include <utility>
using namespace std;
int n,m;
int p[100][100];
bool check[100][100];
int dx[] = {-1,0,0,1};
int dy[] = {0,-1,1,0};
void bfs(int sx, int sy) {
queue< pair<int,int> > q;
q.push(make_pair(sx,sy));
check[sx][sy] = true;
int ct = 0;
while(!q.empty()) {
//printf("-----------\n");
/* 업데이트 되는 판의 모습을 살펴 볼 수 있다.(debugging 용)
for(int i=0;i<n;i++) {
for(int j=0;j<m;j++) {
printf("%d",p[i][j]);
}
printf("\n");
}
//printf("-----------\n");
pair<int,int> f = q.front();
int x = f.first;
int y = f.second;
q.pop();
for(int i=0;i<4;i++) {
int nx = x+dx[i];
int ny = y+dy[i];
if(nx>=0 && nx<n && ny>=0 && ny<m) {
if(check[nx][ny]==false && p[nx][ny]==1) {
//printf("nx ny : %d %d \n",nx,ny);
check[nx][ny] = true;
// 여기서 이전의 값에 +1 을 한 값을 다음 노드에 할당한다
p[nx][ny] = p[x][y] + 1;
q.push(make_pair(nx,ny));
}
}
}
}
// n,m 의 값을 출력한다. 이것은 즉 여기까지 오는데 걸린 최소 거리가 된다.
printf("%d",p[n-1][m-1]);
}
int main() {
scanf("%d %d",&n,&m);
for(int i=0;i<n;i++) {
for(int j=0;j<m;j++) {
scanf("%1d",&p[i][j]);
}
}
bfs(0,0);
}
숨바꼭질 (1697번 문제)
그래프 문제가 아닌거 같은데, 그래프로 변환해서 풀어야 하는 문제이다.
이 문제에서 N에서 K까지 가는 최소 시간을 구해야 한다.
X 와 연결된 노드는 X+1,X-1,2 * X 가 있다.
이 문제는 다음 노드로 이동할 수 있는 가지수가 다음과 같이 수식으로 나타나 있기 때문에, 따로 인접리스트나 행렬을 만들지 않아도 된다. 바로 BFS에 적용하면 된다.(if else 또는 switch case 로). 또한 몇번만에 방문했는지 확인하기 위해 추가적으로 dist[i] 전역 배열 변수가 필요하다.
마찬가지로 dist[시작점] 에 0을 저장하고, 다음 노드에 하나씩 더해가며 queue 에서 마지막 도착점이 나올 때까지 bfs를 진행한다. 마지막에는 dist[도착점] 의 값을 출력해주면 된다.
#include <stdio.h>
#include <queue>
using namespace std;
int n, k;
bool check[100001];
int dist[100001];
void bfs() {
queue<int> q;
q.push(n);
check[n] = true;
dist[n] = 0;
while(!q.empty()) {
int f = q.front();
q.pop();
if(f==k) break;
if(f-1 >= 0 && check[f-1]==false) {
dist[f-1] = dist[f] + 1;
check[f-1] = true;
q.push(f-1);
}
if(f+1 <= 100000 && check[f+1]==false) {
dist[f+1] = dist[f] + 1;
check[f+1] = true;
q.push(f+1);
}
if(2*f <= 100000 && check[2*f]==false) {
dist[2*f] = dist[f] + 1;
check[2*f] = true;
q.push(2*f);
}
}
printf("%d",dist[k]);
}
int main() {
scanf("%d %d",&n,&k);
bfs();
}
가중치가 다른 경우의 BFS
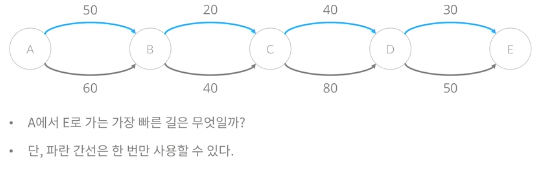
파란 간선을 한번만 쓸 수 있기 때문에 A->B 로 가는 두개의 경로는 다른 경로이다. 파란 간선을 써버렸다면 그 이후에는 쓸수없고, 쓰지 않았다면 그 후에 쓸 수 있기 때문.
따라서 파란간선을 사용한 횟수에 따라서 그래프를 다르게 구해주어야 한다.
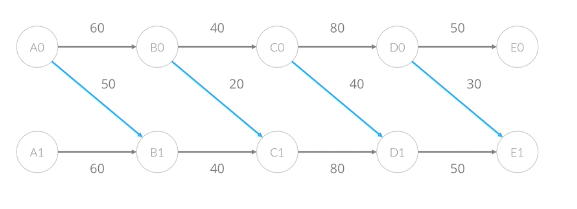
위의 예제는 가중치가 다른 그래프에서 정점을 쪼개는 연습을 해본 것이다. 다음 이모티콘 문제를 통해 연습해보자.
이모티콘 (14226번 문제)
이 문제는 클립보드에 있는 이모티콘의 개수에 따라 다음 정점이 정해지게 된다.
중요한 포인트 : 이모티콘이 클립보드에 몇개가 저장되어 있는가
정점을 (화면개수, 클립보드개수) 로 표현한다고 치자 다음과 같이 노드 사이의 로직을 정리할 수 있다.
복사 연산 : (s, c) -> (s, s)
붙여넣기 연산 : (s,c) -> (s+c,c)
삭제 연산: (s,c) -> (s-1,c)
이 연산을 적용하여 bfs 를 수행한다. 여기에서 클립보드에 있는 값은, 결과자체에 중요한 값이 아니지만, 연산에 있어서 필요한 값이다. 따라서 정점(노드) 는 클립보드의 값이 포함된 (s,c) 로 구성하되, 결과 최솟값을 구할 때는 마지막에 모든 s==S 인 pair 중에 가장 cost 가 작은 값을 골라주면 된다.
코드는 다음과 같다
#include <stdio.h>
#include <string.h>
#include <queue>
#include <utility>
using namespace std;
int S;
int dist[1001][1001];
// 노드의 이동 목록
// (s,c) => (s,s)
// (s,c) => (s+c,c)
// (s,c) => (s-1,c)
// 초기값은 (1,0)
void bfs() {
queue< pair<int,int> > q;
q.push(make_pair(1,0));
dist[1][0] = 0; //초기값이므로 이동x
while(!q.empty()) {
pair<int,int> f = q.front();
q.pop();
int s = f.first;
int c = f.second;
if(dist[s][s]==-1) {
dist[s][s] = dist[s][c] + 1;
q.push(make_pair(s,s));
}
if(s+c<=1000 && dist[s+c][c]==-1) {
dist[s+c][c] = dist[s][c] + 1;
q.push(make_pair(s+c,c));
}
if(s-1>=0 && dist[s-1][c]==-1) {
dist[s-1][c] = dist[s][c] + 1;
q.push(make_pair(s-1,c));
}
}
// 마지막에 모든 S 를 만들 수 있었던 경우의 수 중 가장 작은 cost 를 선택한다
int result = -1;
for(int i=0;i<1001;i++) {
if(dist[S][i]!=-1) {
if(result==-1 || result > dist[S][i]) {
result = dist[S][i];
}
}
}
printf("%d",result);
}
int main() {
memset(dist,-1,sizeof(dist));
scanf("%d",&S);
bfs();
}
덱 사용하기
Double Ended Queue : 양쪽에서 push pop 을 진행하는 큐
숨바꼭질3 (13549번 문제)
기존의 BFS 를 활용한 방법(큐 두개 사용)
BFS 문제는 모든 가중치가 1일때(같을때) 풀 수 있다고 했는데, 가중치가 0인 경우에도 풀 수 있는 경우가 있다.
이 문제에서는 순간이동이 0초가 걸린다.
예시로 5에서 17로 가는 경우 0~20까지만 위치가 있다고 가정한다면, 0초가 걸리는 queue 와 1초가 걸리는 queue 를 나누어서 풀어주면 된다.
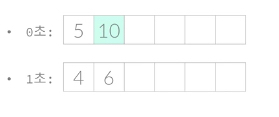
처음 시도에서 0초가 걸리는 작업은 10이고, 1초가 걸리는 작업은 4와 6이다.
그 다음 시도에서 0초가 걸리는 작업은 20이고, 1초가 걸리는 작업은 19과 21이다.
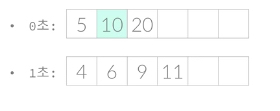
마지막 시도에서는 0초의 작업이 불가능하다(20을 넘어가기 때문에). 따라서 1초의 작업 19만 가능하게 된다.
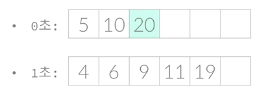
이 작업이 끝나게 되면 0초 큐에 존재하는 모든 작업을 수행했다고 보아도 된다. 이제 남는 것은 1초큐에 있는 작업인데, 이 1초큐에 있는 작업을 바탕으로 다시 2초큐를 만들어 하나씩 똑같이 수행하면 된다.
1초 큐에 있는 4를 0초 작업 하여 8을 추가하고, 2초 큐에 3을 추가한다. 5는 추가할 수 없는데, 그 이유는 이미 방문했기 때문(check 배열에 true 로 존재)이다.
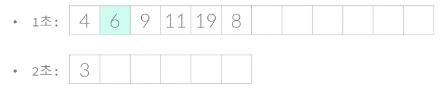
여기서 queue 를 계속해서 만드는 것이 아니라, 0초큐가 비어있게 되면 1초큐의 내용을 가져다가 붙여넣고, 새롭게 1초 큐를 만들어 주는 방식으로 queue를 두개만 사용한다
queue<int> q;
queue<int> next_queue;
// BFS 처리
if(q.empty()) {
q = next_queue;
next_queue = queue<int>(); // 비어있는 큐 생성
}덱을 사용한 방법
BFS 는 어떤 기준을 중심으로 가중치가 1차이 나는 문제를 해결할 수 있다. 따라서 덱을 사용해서 가중치가 0인(순간이동) 작업을 기준 노드의 앞에 배치하고, 1인 작업을 기준 노드의 뒤에 배치하는 방식으로 진행하면 그대로 BFS를 사용하여 풀 수 있다.
이게 왜 가능한지 해석해보면, BFS에서 같은 가중치(같은 레벨)를 가지는 노드들은 뭐가 먼저 실행되어도 상관이 없기 때문에, 0초 작업인 순간이동을 queue 의 앞에 배치하면 결국 현재 노드와 동일한 레벨의 원소를 하나 더 만드는 것이 되기 때문에 가능하다
코드는 숨바꼭질 코드와 정확하게 동일하지만, deque 를 사용하기 때문에 일반적인 pop() 이 pop_front() 가 된다는 점과 push() 가 push_front(), push_back()으로 나누어 진다는 것을 명심해야 한다.
알고스팟 (1261번 문제)
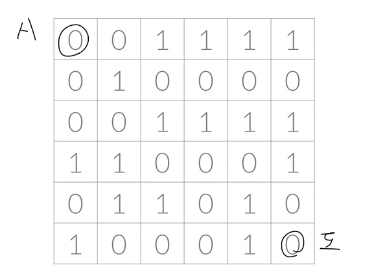
0 은 빈방이라 그냥 이동하고 1은 부수면서 이동하는 것인데, 시작점에서 도착점까지 최소로 벽을 부신 횟수를 구해야 한다.
여기서 빈방을 이동하는 것은, 가중치가 없다(0). 벽을 부수는 행위는 가중치가 1이다.
그렇다면 덱을 이용해서 가중치가 없는 노드의 이동은 큐의 앞에 배치하고, 가중치가 1인 노드의 이동을 큐의 뒤에 배치하면서 BFS를 풀어나가면 된다.
코드는 다음과 같다
#include <stdio.h>
#include <queue>
#include <deque>
#include <utility>
using namespace std;
int n,m;
int dist[100][100];
int check[100][100];
int dx[] = {-1,0,0,1};
int dy[] = {0,1,-1,0};
void bfs() {
deque< pair<int,int> > q;
q.push_back(make_pair(0,0)); //시작값
check[0][0] = true; //시작값 초기화
while(!q.empty()) {
pair<int,int> f = q.front();
q.pop_front();
int x = f.first;
int y = f.second;
for(int i=0;i<4;i++) {
int nx = x+dx[i];
int ny = y+dy[i];
if(nx>=0 && nx<n && ny>=0 && ny<m && check[nx][ny]==false) {
if(dist[nx][ny]==0) {
check[nx][ny] = true;
dist[nx][ny] = dist[x][y];
q.push_front(make_pair(nx,ny));
}
else if(dist[nx][ny]==1) {
check[nx][ny] = true;
dist[nx][ny] = dist[x][y]+1;
q.push_back(make_pair(nx,ny));
}
}
}
}
printf("%d",dist[n-1][m-1]);
}
int main() {
scanf("%d %d",&m,&n);
for(int i=0;i<n;i++) {
for(int j=0;j<m;j++) {
scanf("%1d",&dist[i][j]);
}
}
bfs();
}
벽 부수고 이동하기 (2206번 문제)
벽은 한번만 부수고 지나갈 수 있다. 따라서 벽을 부수는 행위에 따라 노드의 이동이 달라지기 때문에 이 행동을 기준으로 노드의 로직을 생성한다.
(r,c,f) 에서 r 과 c 를 행렬의 위치로 나타내고, f를 벽이 부순적이 있는지 없는지를 나타내는 변수로 두고 로직을 생성하자. 여기서 pair<int,int,int> 를 생성해주면 된다.
앞 뒤 좌 우 4방향으로 움직일 수 있는 것은 제외하고 로직을 기술해 보면
- (r,c,0) -> 벽을 부수거나 부수지 않고 이동이 가능
- (r,c,1) -> 벽을 부수지 않고만 이동이 가능
이렇게 나타낼 수 있다.
나머지는 동일하게 BFS 를 진행해 주면 된다.
탈출 (3055번 문제)
여기서는 고슴도치가 이동함과 동시에 물이 차게 된다. 두개의 BFS를 동시에 구하는 것이 아니라, 물이 차는 시간에 대한 BFS를 모두 구해준 다음, 그 구해진 판과 고슴도치의 경로를 비교하여 구하게 된다.
- 먼저 물이 차는 BFS를 생성한다
- 고슴도치가 이동하는 BFS를 구하는데, 이동했을때의 cost 가 물이 찬 cost 보다 작아야만 이동이 가능하다.
순차적으로 BFS 를 구해준다고 생각하면 쉽다.
코드는 다음과 같다.
while (!q.empty()) {
int x, y;
tie(x,y) = q.front(); q.pop();
for (int k=0; k<4; k++) {
int nx = x+dx[k];
int ny = y+dy[k];
if (nx < 0 || nx >= n || ny < 0 || ny >= m) {
continue;
}
if (water[nx][ny] != -1) continue;
if (a[nx][ny] == 'X') continue;
if (a[nx][ny] == 'D') continue;
water[nx][ny] = water[x][y] + 1;
q.push(make_pair(nx,ny));
}
}
memset(d,-1,sizeof(d));
q.push(make_pair(sx,sy));
d[sx][sy] = 0;
while (!q.empty()) {
int x, y;
tie(x,y) = q.front(); q.pop();
for (int k=0; k<4; k++) {
int nx = x+dx[k];
int ny = y+dy[k];
if (nx < 0 || nx >= n || ny < 0 || ny >= m) {
continue;
}
if (d[nx][ny] != -1) continue;
if (a[nx][ny] == 'X') continue;
if (water[nx][ny] != -1 && d[x][y]+1 >= water[nx][ny]) continue;
d[nx][ny] = d[x][y] + 1;
q.push(make_pair(nx,ny));
}
}
Comments