Compiler Design : Lexical Analysis
2018년도 2학기 연세대학교 Compiler Design Lexical Analysis 수업내용이다
Compiler에서 Scanner의 Token 생성방법과 알고리즘을 배운다
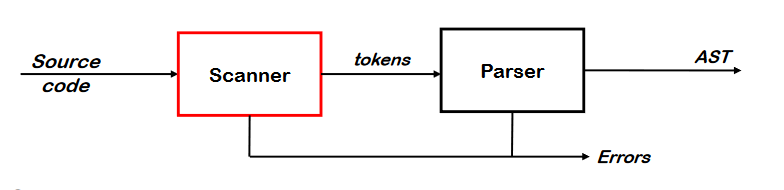
Lexical Analysis
The Role of the Scanner
- 소스코드의 캐릭터를 토큰으로 변환한다.
- <id,x> <=> <id,y> <+> <int literal,21><;> 등등으로 바꾼다
- lexeme이란 단어를 구성하는 캐릭터이다. 패턴에 의해 매칭된 문자열
- 토큰은 튜플이다. <Token_type, value>
Tokens
- MiniC 토큰의 types
- identifier : i, j, initial, position 등의 변수를 말한다
- keywords : if, for, int, float, bool 등의 함수 및 기능들
- operators : +, -, * , &&, <= 등의 연산자
- seperators : {},(),[],;,등의 구분자
- literals : integer literals, float, bool, string 등의 값(value)
- 각각의 토큰은 언어에 따라 달라진다.
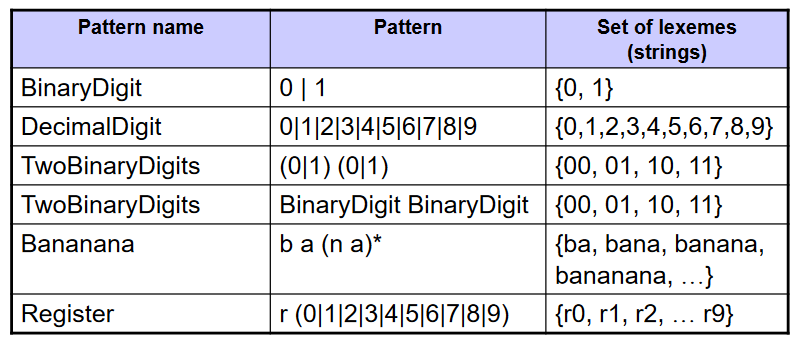
Tokens can be described by patterns
-
Pattern : 특정 토큰 타입의 lexeme 을 설명하는 규칙
INTLITERAL,ID,+,if 등
-
패턴은 세트 안에 있는 각 문자열에 맞아야 한다.
-
formal notation 이 필요하다
프로그래밍 언어의 토큰을 구체화하게 한다.
- 특정 패턴 X에 의해 설명된 lexeme은 X의 언어라고 한다.(language of X)
- we write L(X) to denote the language of pattern X => Pattern 이 X 이고 lexemes 들의 집합이 L(X)이다
String Concatenation
ex) x and y are strings, xy is the string formed by appending y to x
ex) key + board = keyboard
Set Operations
-
Examples
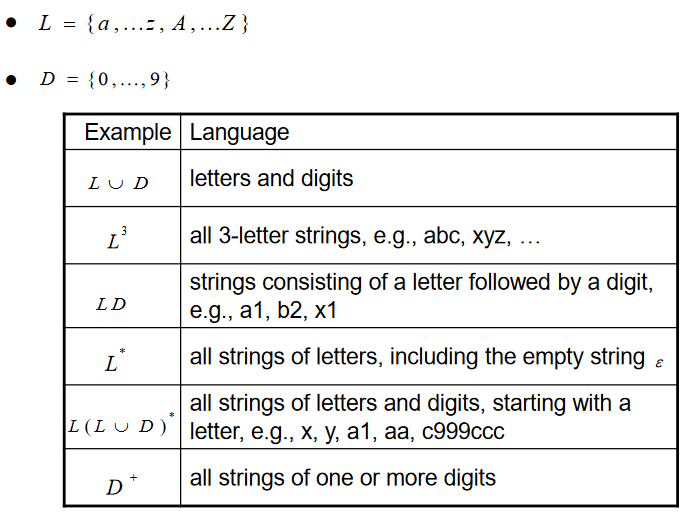
Regular Expressions (inductive definition)
-
REs 는 pattern 을 묘사하는데 사용된다
-
Regular expression r 은 lexeme 들의 집합인 L(r) 을 묘사하는 패턴이다
-
lexeme 들은 alphabet(시그마로 표현됨) 의 character로 부터 만들어진다. alphabet 으로 부터의 character 들을 ++밑줄++ 그어서 표현한다(notation)
-
R1 : epsilon 는 epsilon 세트를 의미하는 RE 표현이다
-
R2 : 만약 ++a++ 가 alphabet 에 있다면 ++a++ 의 RE 표현은 {++a++} 를 의미한다
L(++a++) <=> {++a++}
-
R3 : 만약 x 와 y 가 RE 표현으로 L(x) 와 L(y) 를 의미한다면, x y 는 L(x) cup L(y) 를 뜻한다 (Alternation) -
R4 : 만약 x 와 y 가 RE 표현으로 L(x) 와 L(y) 를 의미한다면, xy 는 L(x)L(y) 를 뜻한다 (Concatenation)
- R5 : 만약 x 와 y 가 RE 표현으로 L(x) 와 L(y) 를 의미한다면, x* 는 L(x)* 를 뜻한다 (Repetition,Closure)
-
-
Examples1
Precedence Rules
-
Precedence rules 은 RE의 모호함을 없애는 것에 필요하다
ex)
a + b * c = a + (b * c)Parenthesis 를 사용해서 해결할 수 있다
-
Precedence of regular expression operators is closure, then concatenation, then alternation
Example Token Specifications using REs
Writing Regular Expressions
-
Ruby binary literals : binary number 앞에는 “0b” 가 존재한다. 그리고 한쌍의 binary digit 사이에 userscore 가 포함될 수 있다. 그러나 underscore 앞 뒤에는 digit 이 꼭 존재해야 한다.
0b001011, 0b010b0_101, 0b11_01NOT*&
0b_1, 0b1_ -
Ada identifiers : letters, digits, underlines 사용이 가능하지만
_A나A__B등은 불가능하다.A letter followed by any number of letters, digits, and underlines. An identifier must not end in an underline or have two underlines in a row.
letter(letter|digit)* (_|epsilon) (letter|digit)* -
A floating point number : decimal point 다음에는 하나 이상의 digit이 와야한다.
(+|-) digit (digit)* (.) digit (digit)* -
Floating point number in scientific notation : e나 E가 decimal point 한자리 뒤에 와야 한다.
(+|-) digit (digit)* (.) digit (((e|E) (+|-|epsilon))(digit)*|epsilon) (digit)*
Shorthand Notations
- 하나 이상의 concatenations : r^+^ = rr*
-
없거나 하나의 instance : r? = epsilon r. 표현하면 L(r) cup {epsilon} 과 같다 - 캐릭터 classes : [a-z A-Z]
MiniC RE Examples
| token | RE |
|---|---|
| letter | [a-z A-Z_] |
| identifier | letter(letter|digit)* |
| integer | digit* |
- miniC에서는 letter가 _ 를 포함한다
- Java 에서는 유니코드를 캐릭터셋으로 사용가능하다 (한글이 가능하다)
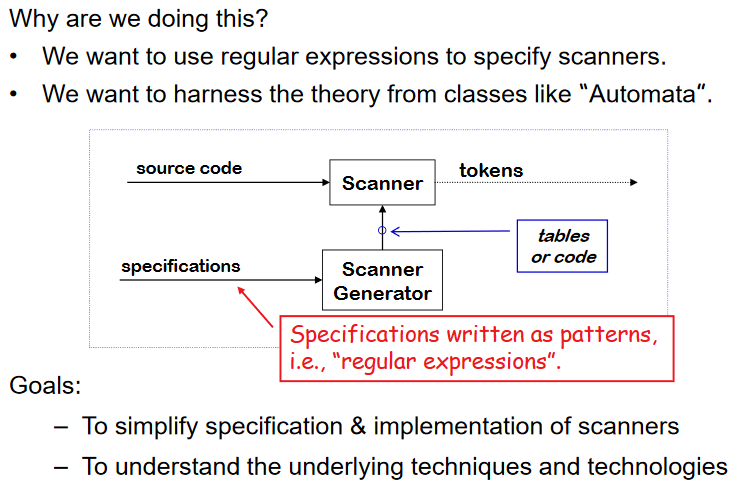
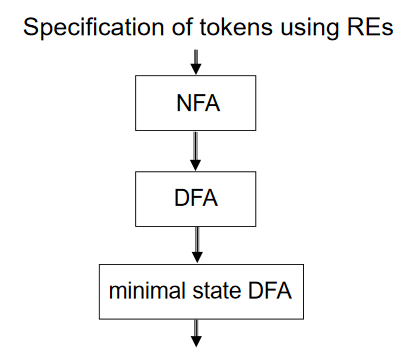
The Big Picture
- 스캐너가 source code를 토큰으로 바꾸고 패턴으로 쓰여진 specification을 scanner generator가 scanner 에 전달한다.
- scanner의 행위를 automate 한다 (시간 절약)
Regular Expressions
- REs 를 사용하여 lexeme 의 mapping 을 token으로 구체화할 수 있다.
- Automata 이론과 알고리즘 이론을 사용해서 RE 로부터 recognizer 를 자동으로 만들 수 있다.
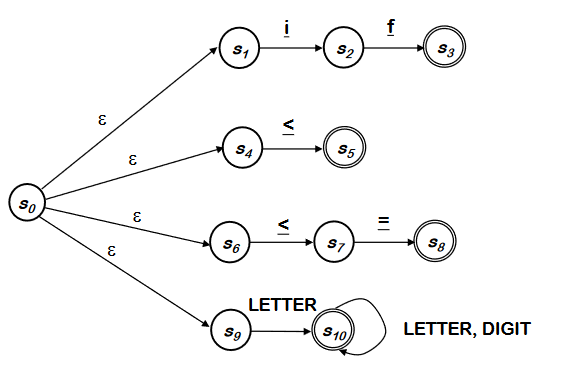
Example
-
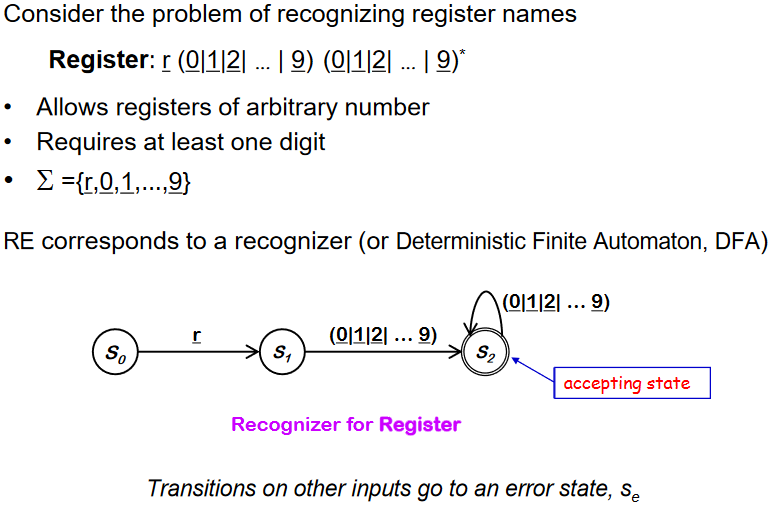
그림에서의 S~0~ 는 initial state(start state) 이고 받은 input을 확인한다. 그리고 S~1~으로 이동한다.
-
S~1~는 input에서 decimal digit 을 찾아서 S~2~로 이동한다
-
S~2~ 는 accepting state이다. self transition을 진행(반복)하기도 한다. 유효한 것인지 확인한다.
-
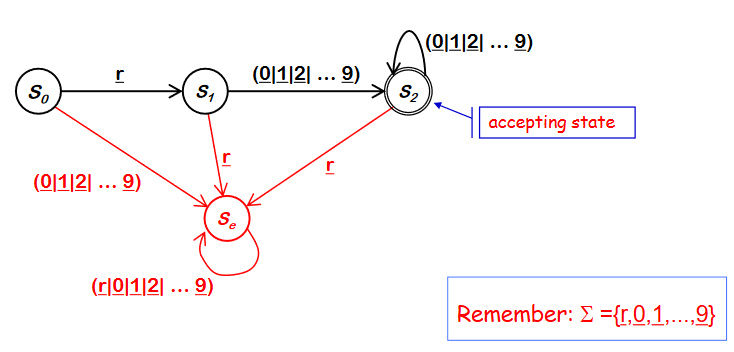
만약 유효한 accpeting state 가 아니라면 S~e~ 로 이동한다. 한번 error state로 가면 돌아올 수 없다. 그냥 오류. 어떤 state에서도 error state로 이동할 수 있다.
ex) digit이 먼저오면 이동(r이 아닌경우)
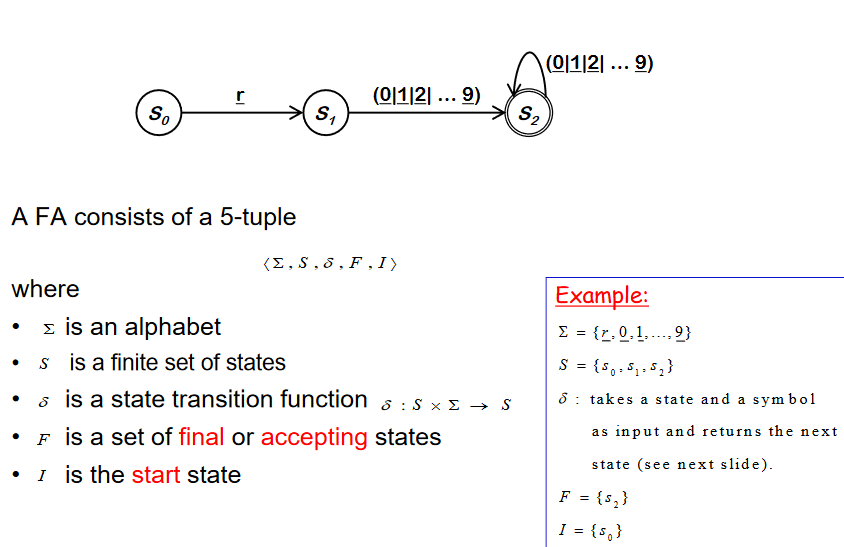
Finite Automata (FA)
State Transition Function and Code
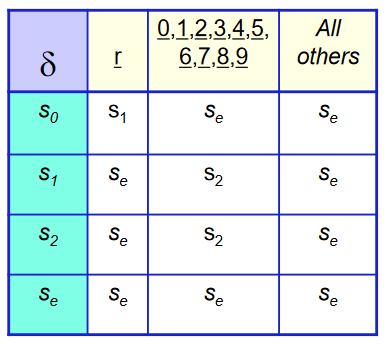
- Table encoding RE
- Skeleton recognizer
char <- next character
state <- s0
while(char!=EOF) //as long as we have input
state <- delta(state,char)
char <- next character
if(state is a final state) return success
else return failure
Non-deterministic Finite Automata (NFAs)
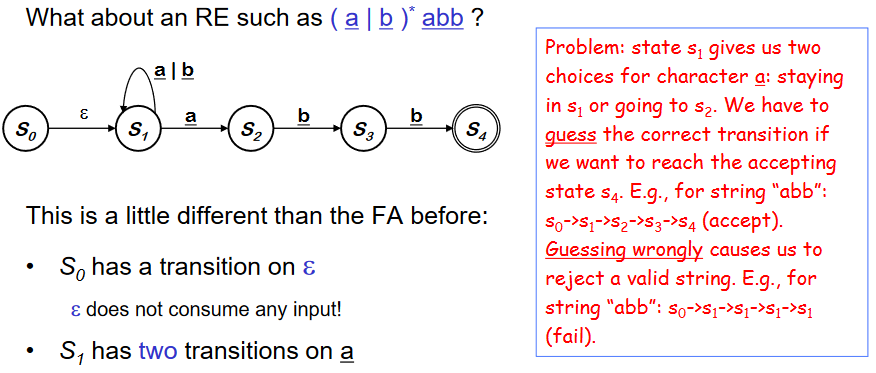
- 맨앞에 epsilon 이 있으면 S~0~ 에서 S~1~로 이동.
- S~1~은 두개의 transition을 가진다. (a에서)
- 이런 것을 Non-deterministric finite automaton (NFA) 라 한다.
- NFA는 table에서 결정할 수 있는 것이 확실하지 않다.
- NFA는 두개의 NFA를 합치기 쉽다.( epsilon 을 사용해서) 이것을 epsilon -transition이라고도 한다.
Relationship between NFAs and DFAs
DFA는 NFA의 특별한 케이스이다.
-
DFA는 epsilon transition 이 없으며 하나의 state에서 어떤 두개의 transition이 존재하지 않는다.
-
DFA는 NFA로 나타낼 수도 있다.(당연히)
-
NFA는 DFA로 나타낼 수 있다.
가능한 state들을 시연한다. 단 하나의 character input 당 하나의 state 가 나타나야 한다.
Summary : NFAS and DFAs
A FA is a DFA if
어떠한 state도 epsilon -transition 이 없다. 다시 말해 epsilon 인풋에는 trainsition이 존재하지 않는다. Input symbol ++a++ 에 대해 각 state s 마다 s state를 떠나는 최대 한개의 edge 가 존재한다.
A FA is an NFA
epsilon -transition 을 포함하거나, Input symbol ++a++ 에 대해 state s 에서 여러개의 가능한 transition 이 존재할 경우이다.
Automating Scanner Construction
Specification 을 코드로 변환하기 위해서는
- Input language 에 따른 RE 를 적는다.
- 큰 NFA를 만든다.
- NFA를 돌게하는 DFA를 만든다.
- DFA의 state 개수를 최소화한다.
- Scanner code 를 생성한다.
Scanner generators
- Lex 와 Flex 가 있다.
- 알고리즘이 필요하며 주요 issue 는 parser 로의 interface 이다.
Outline
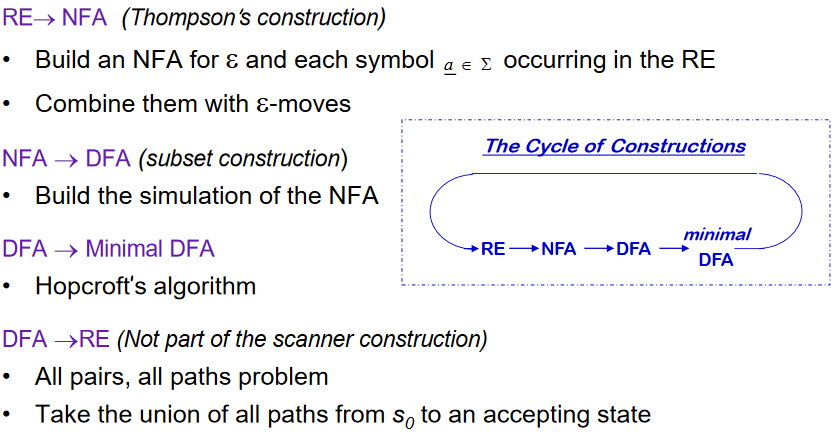
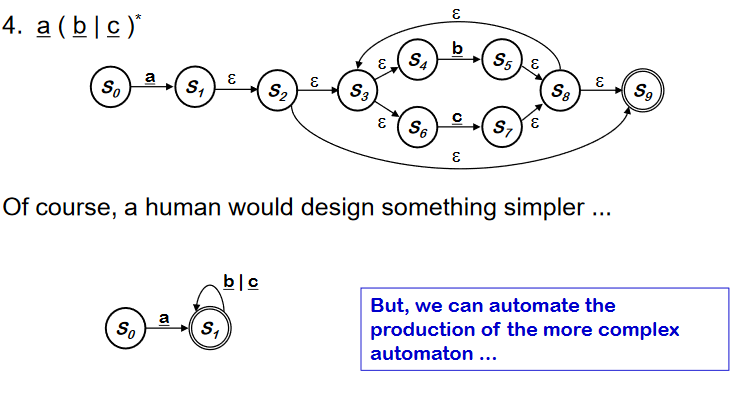
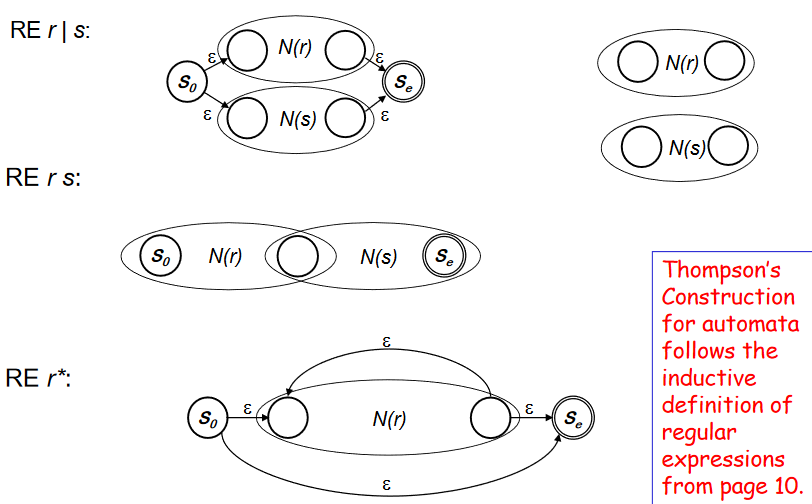
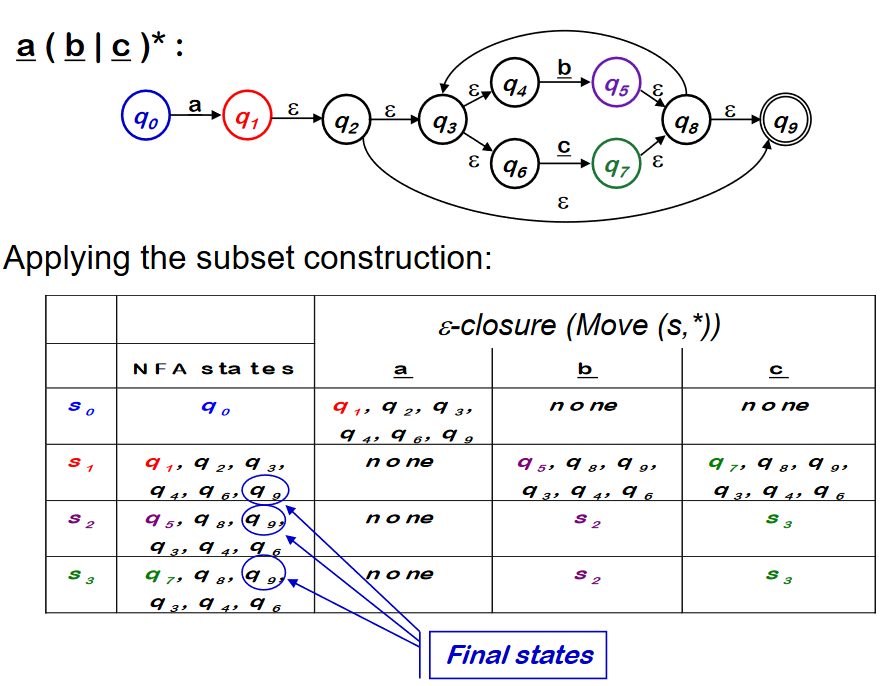
RE -> NFA using Thompson’s Construction
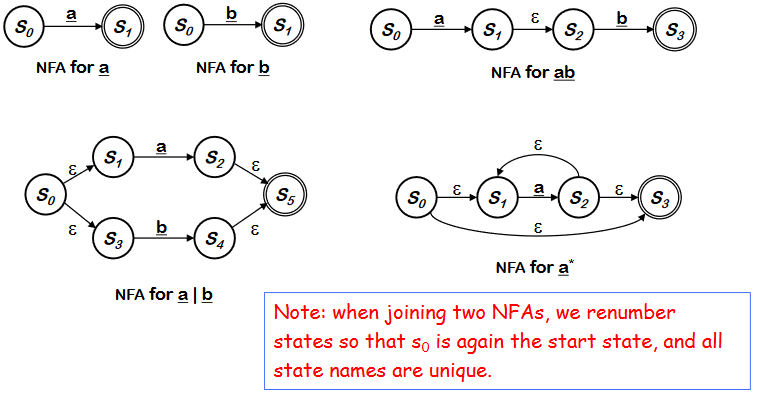
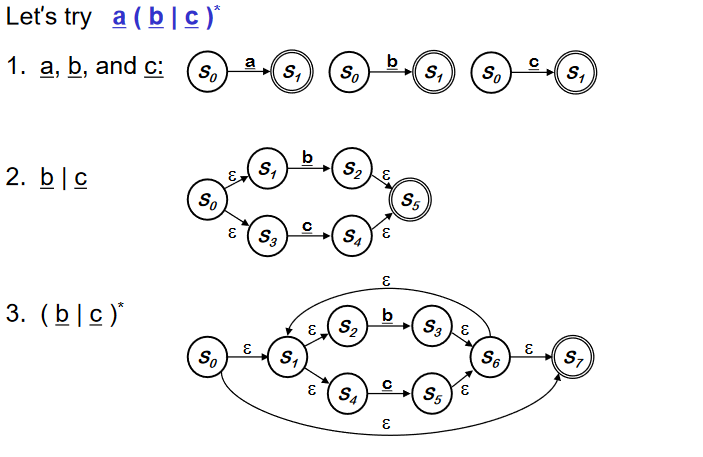
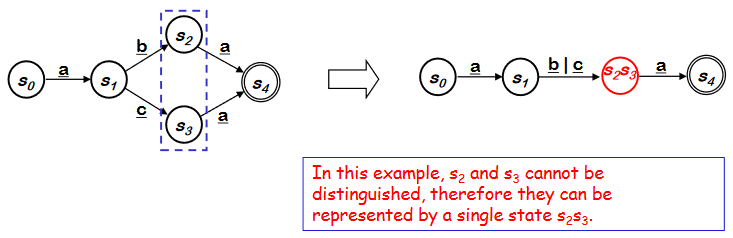
RE 의 각 symbol 과 operator 를 NFA 로 구성하고 epsilon 을 사용하여 RE의 precedence order 에 따라 합친다. NFA를 합칠 때, state 번호를 재 부여해서 S~0~ 가 start state 가 될 수 있게 하고, 각 state 의 이름은 unique 하게 한다.
위와 같이 사람은 더 간단하게 만들 수는 있지만, production 을 automate 하는 것에 중점을 맞추자
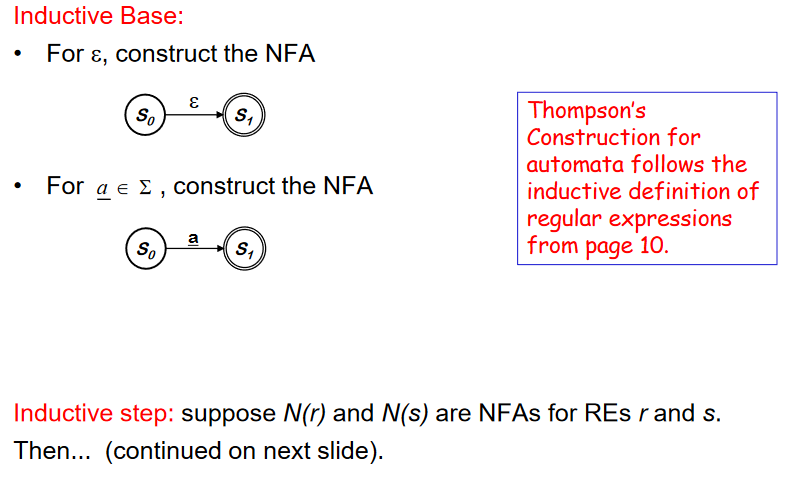
Thompson’s Construction
- Syntax-driven 이다. REs의 구조를 가진다
- Inductive Base
- REs 의 정의에 의해 NFA 가 구성된다.
- Inductive step 에서 작은 NFA로 bigger NFA를 만든다.(입실론을 사용해서)
- Important : 만약 RE r 에서 symbol ++a++ 가 여러번 나타나면 각각의 ++a++ 에 대해 별도의 NFA를 구성해야 한다.
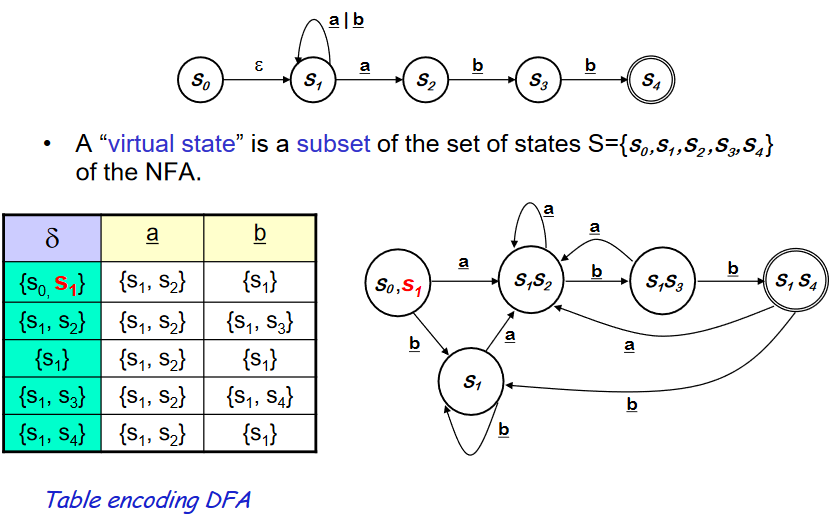
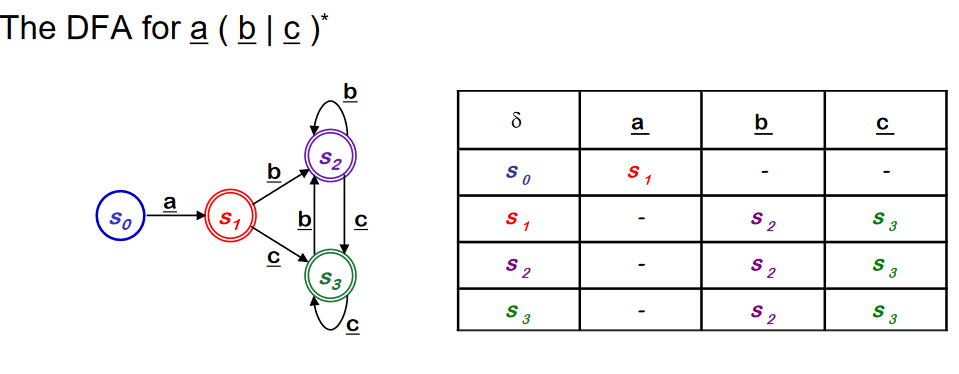
Subset Construction (NFA -> DFA)
- S~1~ 에서 a 가 재귀하는지 S~2~로 가는지 확신할 수 없다. 그러므로 두개의 transition을 병행하여 따라간다.
- virtual state 라는 것을 만들어서 symbol ++a++ 가 input 일 때 가능한 S~1~ 의 trainsition 인 S~1~과 S~2~를 포함하게 한다.
- virtual state 는 모든 states의 subset 이다.(non-empty)
- {S~0~,S~1~} 는 start state. 이녀석이 가질 수 있는 가능성은 a로 갈 경우 {S~1~,S~2~} 가 될 수 있고, b로 갈 경우에는 S~1~밖에 존재하지 않는다.
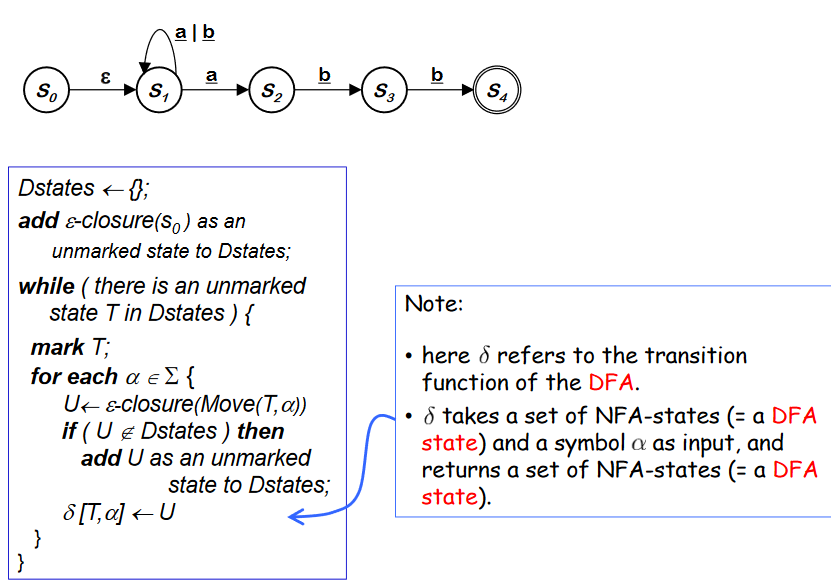
Alogorithm : NFA -> DFA with Subset Construction
On-the-fly simulation 은 RE 가 한번만 사용될 경우 유용하지만 컴파일러가 language 의 token을 계속해서 만들어 내야할 경우에는 적절하지 않다. 그래서 Subset Construction 을 사용한다.
Subset Construction 은 NFA state 들에 적절히 이용될 수 있다. 각 NFA state 들은 DFA state 가 된다.
-
Start state에서의 변환은 epsilon-closure 를 가지고 있다. 그러므로 맨 처음에 start state 에 대한 epsilon-closure 값 (set of states reachable from S~0~) {S~0~,S~1~} 을 Dstates 에 넣는다.
여기서 Dstates 란 DFA -> NFA 를 통해 만들어지는 새로운 states 이다.
-
While 문을 보면 Dstates 가 끝날때까지 반복하며, for 문 안에서는 alphabet 에 포함된 모든 character 당 결과 값들을 계산하도록 되어있다. 처음 반복문에 들어오면 T는 {S~0~,S~1~} 이고, 알파는 a 와 b 가 되는데, 알파 a 에 대한 U의 값은 {S~1~,S~2~} 가 되며 이는 기존의 Dstates 에 포함되지 않았기 때문에 추가한다. 또 알파 b에 대한 U의 값은 {S~1~} 이 나타나고 또한 Dstates 에 추가한다. 마지막으로 각 결과 값을 델타에 저장하고 반복문을 위와 같이 반복한다.
위와 같은 Subset Construction 을 통한 NFA -> DFA 의 결과로 table을 만들 수 있고, 각각의 Dstates 를 토대로 새로운 DFA 를 만들어 낼 수 있다. 여기서 기존의 NFA state 에서 accepting state 였던 state 를 포함하는 Dstate 는 모두 새로운 DFA 의 accepting state 가 된다.
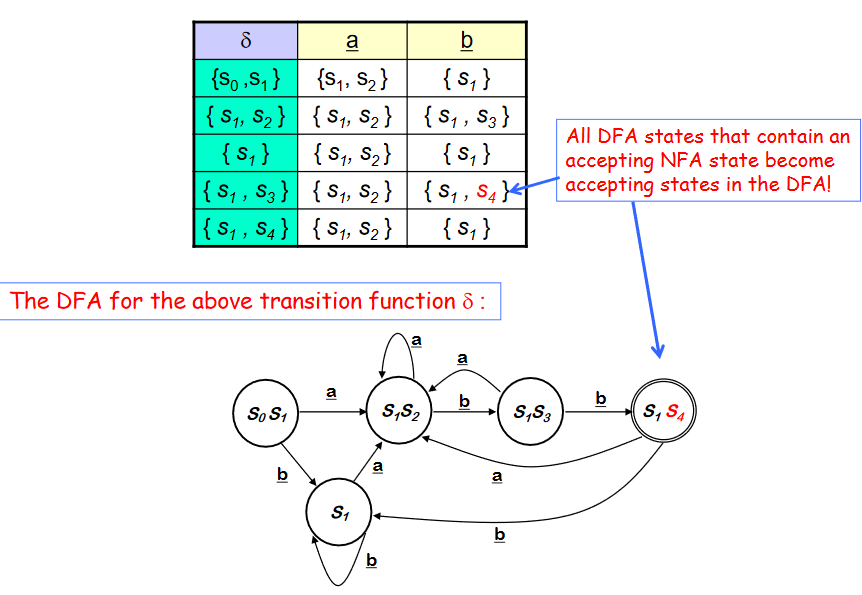
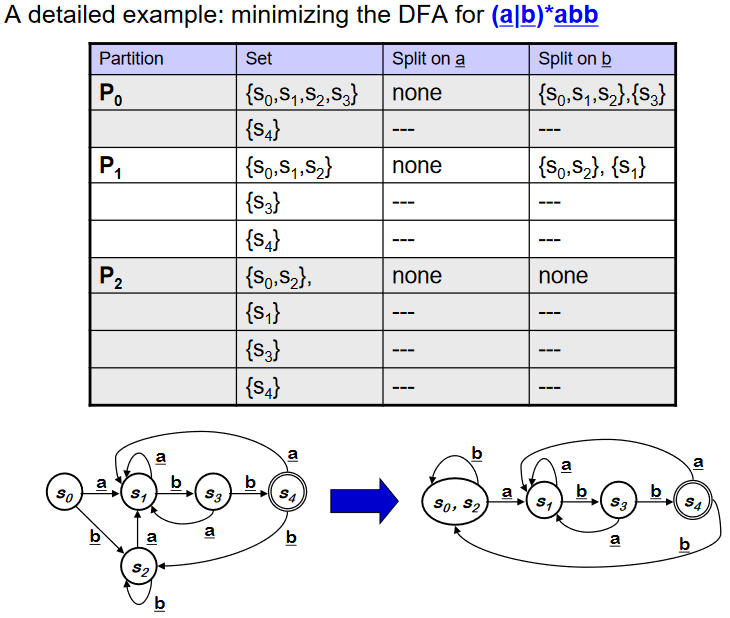
Example : NFA -> DFA with Subset Construction
Subset Construction 에 의해 새롭게 만들어진 DFA 에는 accepting state 가 3개이다.(기존 NFA의 accpeting state 를 포함하는 Dstate 가 3개 이므로). 또한 모든 transition 은 deterministic 으로 변했다.
적은수의 state는 테이블의 관점에서 보았을 때 유리하다(좋다). 이제 DFA를 더 축약하는 알고리즘을 배운다.
DFA Minimization Overview
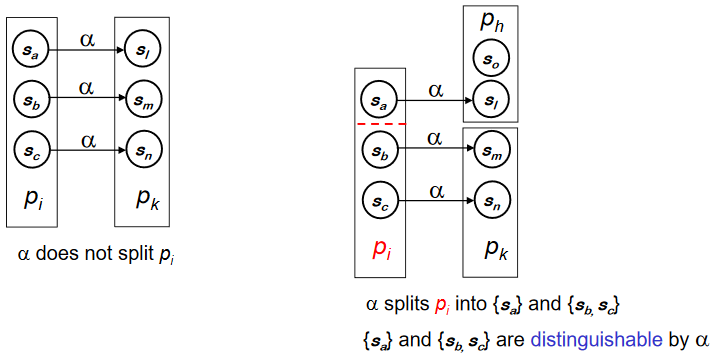
- 다른 state와 구별가능한 state를 찾는다
- 구별되지 않는 state는 하나의 state로 표현한다.
-
두개의 state중 하나는 input 값에 의해 accepting state가 되고 다른 하나는 accepting state가 아닌 곳으로 이동하였을 때, 그 두개는 그 input 값에 대해 구별가능한 state라고 한다.
-
Partition 의 개념
{S0,S1,S2,S3} => {S0,S1},{S2},{S3}
// these sets are divided by partition, S0 and S1 is not distinguished
각각의 state s 는 정확히 하나의 partition p 에 포함된다. 따라서 같은 세트에 있는 state 들은 아직 구별되지 않았다고 하고, 다른 세트에 있는 state 들은 구별되었다고 한다.
ex) 위의 그림에서 s0 와 s1은 구별되지 않았고, 나머지는 구별되었다.
-
초기 partition P 는 두개의 세트를 포함한다.
하나는 Accepting state F 와 non-accepting state S-F 이다. 이 둘은 Empty string epsilon 에 의해 구별될 수 있다.(재귀)
-
Input character 값 (symbol alphabet) 에 따라서 각각의 state 들이 다른 partition 으로 분리되는지 확인한다.
DFA Minimization
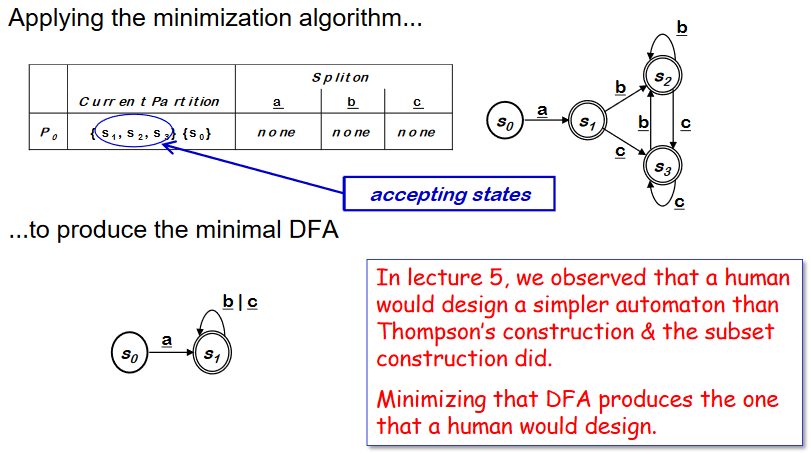
Initial partition P 는 두개의 state를 포함한다.
Partition 이 변형 가능한한 split 를 지속하고 변형된 내용을 partition 에 적용한다.
DFA minimization 의 두가지 불변의 법칙에 의해 알고리즘이 유지된다. 같은 세트에 남아있는 state 들은 어떤 string 에 대해서도 아직 구별되지 않은 state 들이다. 다른 세트로 나누어지는 state들은 어떤 string 에 의해 구별 가능한 state 들이다.
위와 같이 같은 세트에 있는 state 들이 어떠한 symbol input 에 의해서도 나누어지지(split) 않으므로 하나로 합칠 수 있다. 이 결과 Minimal DFA 를 만들어 낼 수 있다.
모든 RE language 는 minimal-state DFA (모든 state 이름들이 unique 한) 로 인식될 수 있다.
Table-driven vs. Direct-coded Scanners
트랜지션 테이블을 기준으로 만든 것이 table-driven scanner 이고, 코드로 직접 짜는 것이 direct-coded scanner 이다.
Effieciency 의 측면에서 바라본 table driven vs direct-coded scanner
Table driven 은 캐시의 문제(cache miss)가 있을 수 있다(만약 table 이 커질 경우)
Scanner Generators
C로 만들어진 scanners
lex(UNIX), flex(GNU’s fast lex, UNIX), mks lex(MS-DOS,Windows,OS/2)
Java 로 만들어진 scanners
JLex (Princenton University), JavaCC(Oracle)
How a Scanner Generator Works
DFA 는 두가지로 표현될 수 있다.
Table-driven code (JLex) 로 표현될 수도 있고, Hard-wired code (직접 짠 코드) 로 표현될 수도 있다.
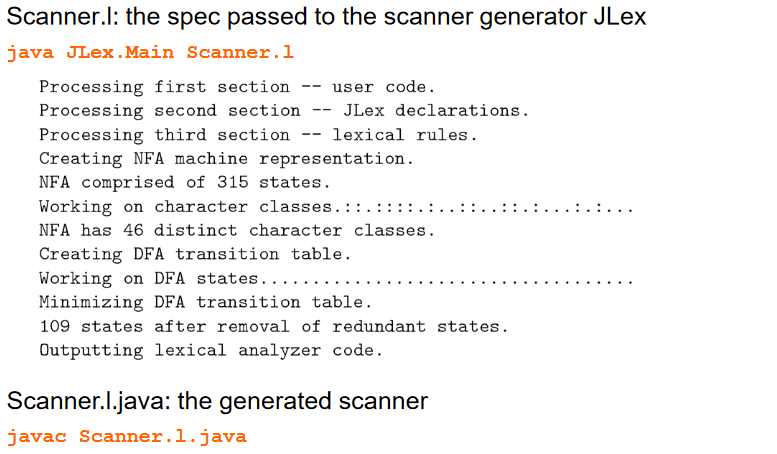
JLex Example Spec
Running JLex on a Sample Scanner Spec
Limitations of Regular Languages
**RE 의 장점 **
- pattern 들을 구체화하는데에 간단하고 강력한 notation
- 빠른 scanner (recognizer) 의 자동 구성
- 많은 pattern 들이 REs 에 의해 구체화 될 수 있음
만약 이렇게 장점이 많다면 왜 모든 것에 RE 를 사용하지 않을까?
- 표현할 수 있는 expression 에 한계가 있다.
- 정해진 N개의 문자열이 오는 경우나, 수학적 표현이나, parentheses match 를 표현할 수 없다.
결론
REs 는 keywords, identifiers, literals, operators 그리고 punctuation character 만 표현할 수 있다. 다른 많은 것들 (expressions, statements, nested statements, …) 은 더 강력한 방법이 필요하다.
Regular Expressions and Context-Free Grammers
REs 와 Context-free grammers 로 정의될 수 있는 언어는 다음과 같은 결론을 갖는다.
-
RE 는 CFGs 보다 약한 formalism 을 가진다. RE 에 의해 표현될 수 있는 언어는 모두 CFG에 의해 표현이 가능하지만 반대는 가능하지 않을 수 있다.
-
RE 에 의해 표현가능한 언어는 regular languages 라고 한다.
-
일반적으로 “self embedding” 을 하는 언어는 RE 에 의해 표현될 수 없다.
-
프로그래밍 언어는 “self embedding” 을 한다.









Comments