Compiler Design : DFA & NFA Quiz
Regular Expression, Design deterministic finite automata, Thompson’s construction algorithm, Subset construction algorithm 를 사용하여 문제를 풀고 있다.
Q. Given the alphabet Σ ={−,+, x, y, z,0,1} and the below regular expression, which strings are valid? (Mark one or more.)
R: (−|+|epsilon) (x|y|(0|1)*) z (0|1)*
(a) −xz1
(b) −xz
(c) yxz
(d) epsilon
(e) 01z−1
(f) +011z1
(g) +x
(h) zx
A. (a), (b), (f)
Q. Given the regular expression below, which strings are valid? (Mark one or more.) Note: “[a−z]” denotes lower-case characters, “[A−Z]” denotes upper-case characters, and “[0−9]” denotes the digits from 0–9.
R: [a−z] ( [a−z] | [A−Z] | [0−9] | _ )*
(a) x_
(b) _x
(c) yx0z
(d) epsilon
(e) ada1
(f) a_d_a_1
A. (a), (c), (e), (f)
Q. Write regular expressions for the following languages whose alphabet is Σ ={0,1}.
(a) All possible strings, including the empty string.
RE : (0|1)*
(b) The empty string.
RE : epsilon
(c) The string 1011
RE : (1011)
(d) The strings 1 and 101.
RE : (1)(101)
(e) All strings beginning with 01.
RE : (01)(0|1)*
(f) All strings that contain exactly two 1’s.
RE : (0)*(1) (0)*(1)(0)*
(g) All strings beginning with a 0 and ending with a 1.
RE : (0)(0|1)*(1)
Q. Design deterministic finite automata (DFAs) to recognize the following languages over the alphabet Σ ={x, y}.
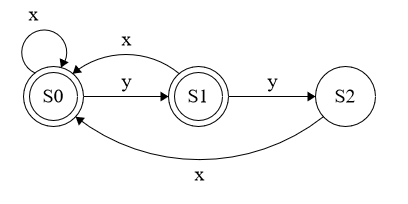
(a) Every occurrence of the substring yy is followed by an x.
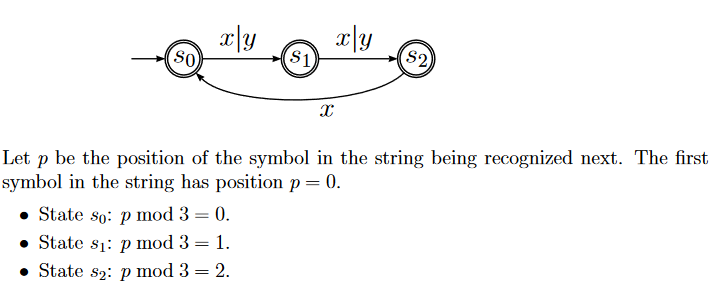
(b) Every third symbol is an x.
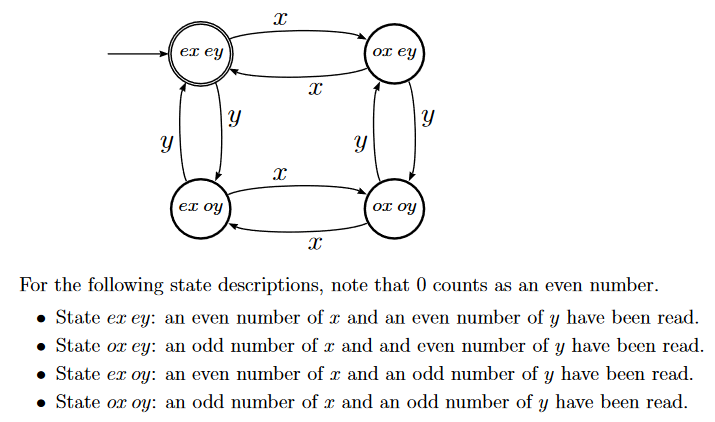
(c) All strings with an even number of x and an even number of y.
When you build an automaton by hand, it is a good idea to add a description to each state: the description should specify which strings can possibly reach that state.
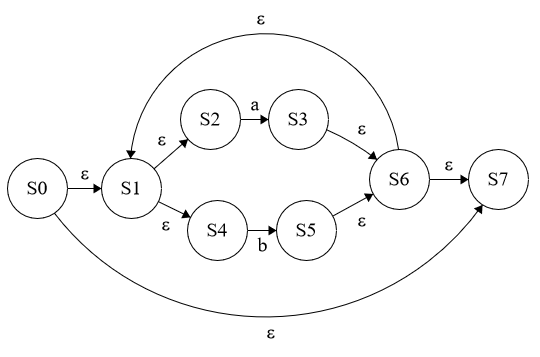
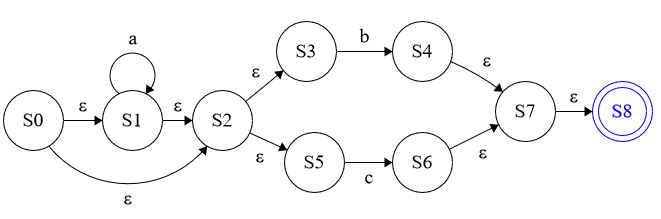
Q. Use Thompson’s construction algorithm to construct non-deterministic finite au-tomata (NFAs) from the following regular expressions:
(a) (a|b)*
위에서 S7 은 accepting state 이다(표현을 하지 못했음)
(b) a*(b|c)
(c) a(a|b)*a
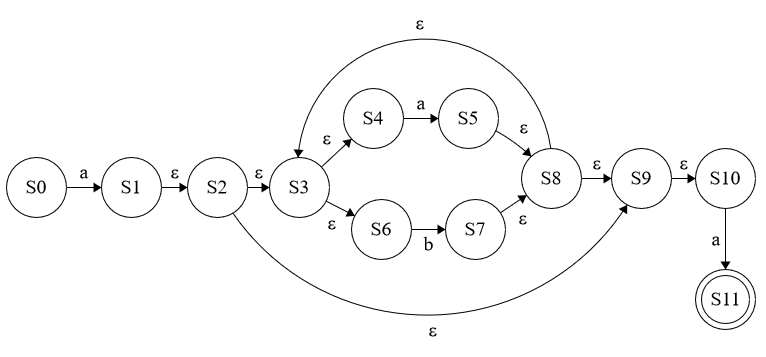
Q. Use the subset construction algorithm to convert the above NFA for a*(b|c) to a DFA.
NFA for a*(b|c)
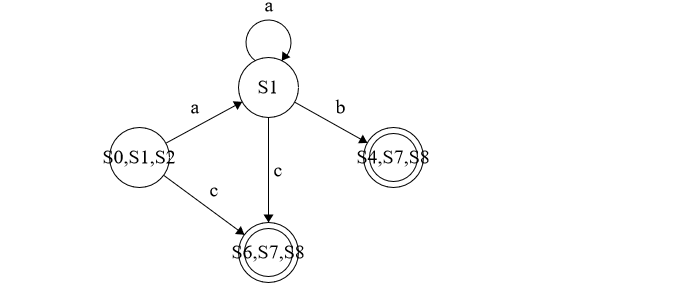
Table encoding DFA
| delta | a | b | c |
|---|---|---|---|
| {S0,S1,S2} | {S1} | {S4,S7,S8} | {S6,S7,S8} |
| {S1} | {S1} | {S4,S7,S8} | {S6,S7,S8} |
| {S4,S7,S8} | None | None | None |
| {S6,S7,S8} | None | None | None |
The DFA for a*(b|c)
Comments